Difference between revisions of "Multi-Axis Kinematics"
m (→Refer to) |
(Changed subsection name and added links) |
||
| (28 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | <div id="BackToTop" class="noprint" style="background-color:; position:fixed; bottom:32px; left:95%; z-index:9999; padding:0; margin:0;"> |
| + | <span style="color:blue; font-size:8pt; font-face:verdana,sans-serif; border:0.2em outset:#ceebf7; padding:0.1em; font-weight:bolder; -moz-border-radius:8px; "> | ||
| + | [[Image:TOP2.png|50px|link=#top]] </span></div> | ||
| + | {{Languages|Multi-Axis_Kinematics}} | ||
= Introduction = | = Introduction = | ||
| − | |||
| − | + | Multiple axes can be combined into groups and moved. There are: | |
| + | * simple groups (no models, can be either homogeneous or non-homogeneous) | ||
| + | * Cartesian groups (role of each axis is strictly defined, e.g.: XYZ, XYZR, ...) | ||
| + | * robots (the specific robot model is applied (SCARA, PUMA, ...) | ||
| − | |||
| − | In non- | + | Groups are data-objects (motion-elements) that enables us to move it's axes together synchronously. In case all axes are of same type (all linear or all rotary) their velocity, acceleration and jerk values can be combined (using a square root of the sum of squares) and the movement parameters will have physical meaning. We call these types of groups '''homogeneous groups'''. |
| + | |||
| + | '''Non-homogeneous groups''' consist of different axes, both rotary and linear. A feature was added to support the definition of velocities for non-homogeneous groups. In the setup, rotary and linear axes are declared. The system determines if it is a linear- or rotary-dominant group. For example, in SCARA robot, there are two rotary axes for the first and second joints and another rotary axis for the last joint (roll). There is only one linear axis (the Z axis). Such a system is rotary-dominant. Another example is the XYZ-Roll system. Here, there are two linear (X & Y) axes and another linear (Z axis) with just one rotary axis (roll). In this case, the system is linearly-dominant. Axis setup defines the group behavior. Each axis must be declared whether it is linear or rotary by setting [[MC-Basic:axis.POSITIONROLLOVERENABLE|'''POSITIONROLLOVERENABLE''']] to either zero(0) for linear or one (1) for rotary. | ||
| + | |||
| + | In non-homogeneous groups, in joint-interpolated movements ([[MC-Basic:MOVE|MOVE]]) commanded velocity is always given according to the group dominance type (See: [[MC-Basic:group.DOMINANCEMODE|DOMINANCEMODE]]). If the group is linearly-dominant, the velocity ([[MC-Basic:element.VELOCITYCRUISE|'''VCRUISE''']], [[MC-Basic:element.VELOCITYFINAL|'''VFINAL''']]) is in linear units (mm/sec). The other non-linear axes are checked in the preparation phase of the movement. The velocity in these axes cannot exceed the maximum value. If it does, the overall (group) velocity is reduced. | ||
There is only one exception to this rule. This is when a group movement is issued with only one axis in motion and all the others are stopped. Then, the given value of the velocity is taken directly in the units for that axis. For example, having movement on the third axis of the SCARA robot, the velocity value is in mm/sec. | There is only one exception to this rule. This is when a group movement is issued with only one axis in motion and all the others are stopped. Then, the given value of the velocity is taken directly in the units for that axis. For example, having movement on the third axis of the SCARA robot, the velocity value is in mm/sec. | ||
| Line 13: | Line 21: | ||
The same is true for both acceleration and jerk values for group-interpolated motion. | The same is true for both acceleration and jerk values for group-interpolated motion. | ||
| − | + | In case the non-homogeneous group is improperly set, means there are axes of different types but the [[MC-Basic:axis.POSITIONROLLOVERENABLE|'''POSITIONROLLOVERENABLE''']] of all of them is set to the same value, the group will still move but the velocity/acceleration/jerk values of the group will have non-physical meaning. In cases the numeric values between the axes differ significantly the system could behave wired. | |
| + | |||
| + | |||
| + | {{Note| The above discussion is valid for simple '''joint-interpolated motion of a group''' only (See [[MC-Basic:MOVE|'''Move''']] or [[MC-Basic:CIRCLE|'''Circle''']]). Commands like [[MC-Basic:MOVES|'''Moves''']] or [[MC-Basic:CIRCLE|'''Circle''']] in Cartesian groups use [[MC-Basic:robot.VELOCITYTRANS|'''Vtran''']] and [[MC-Basic:robot.VELOCITYROT|'''Vrot''']] parameters}} | ||
| + | |||
| + | == Coordinate Systems == | ||
| + | |||
| + | === World coordinate system === | ||
Having different world and joint coordinates make the robot kinematics unique. The world coordinates are normally perceived as working coordinates of an application. Usually, there is some form of Cartesian coordinate system originating in the robot base. | Having different world and joint coordinates make the robot kinematics unique. The world coordinates are normally perceived as working coordinates of an application. Usually, there is some form of Cartesian coordinate system originating in the robot base. | ||
| − | Another set of coordinates is added for the orientation of the end-effector (gripper, etc.). The orientation of a body in space is normally described by three angles. Depending on the number of degrees of freedom (motors used to actuate the orientation joints), they could be unequal. The world space coordinates are given by its position part (X, XY or XYZ tupple), in most cases. In general, it could be anything from sphere coordinates to cylindrical system. The orientation component can use many forms for describing orientation. The | + | Another set of coordinates is added for the orientation of the end-effector (gripper, etc.). The orientation of a body in space is normally described by three angles. Depending on the number of degrees of freedom (motors used to actuate the orientation joints), they could be unequal. The world space coordinates are given by its position part (X, XY or XYZ tupple), in most cases. In general, it could be anything from sphere coordinates to cylindrical system. The orientation component can use many forms for describing orientation. The mostly used coordinate system for orientation angles are the Euler angels: yaw, pitch and roll. Theoretically there are 12 different presentation of Euler angles, depending on the order of orientations in most robot models we are using the Z-Y-Z order. |
| + | |||
| + | === Joint Coordinate system === | ||
The joint space of a robot is a relatively simple concept. A joint coordinate is a number uniquely describing the position of a robot segment relative to the previous robot segment. If the joint connecting the segment is rotary, the joint coordinates are in degrees of the rotation angle. If it is linear, the joint coordinates are the linear displacement (millimeters). | The joint space of a robot is a relatively simple concept. A joint coordinate is a number uniquely describing the position of a robot segment relative to the previous robot segment. If the joint connecting the segment is rotary, the joint coordinates are in degrees of the rotation angle. If it is linear, the joint coordinates are the linear displacement (millimeters). | ||
| − | |||
| − | The different coordinate systems are implemented as variables of different data types. Generally, a point in a coordinate system is defined as a point data type. Depending on if it is a joint space or world space, the sub-type of the point differs. There is a point data type with two | + | == Point Data Type == |
| + | |||
| + | The concept of joint coordinates is an ''n''-tupple number. Each number represents the coordinate of the specific joint. The world coordinates are supported by different built-in types (XY, XYZ, XYZR) that describe each of the different world space representations. There can be different world space descriptions for the same (or same dimensional) world coordinates. Each robot has its default world-space type. Different robots could have same world space types, as long as they have same number of degrees of freedom ('''NDOF'''). For example, xy-table world space has XY world space descriptors. A SCARA robot having a Z axis for vertical motion and a roll axis for orientation uses world frame coordinates consisting of: X, Y, Z and roll or an XYZR descriptor. | ||
| + | |||
| + | The different coordinate systems are implemented as variables of different data types. Generally, a point in a coordinate system is defined as a point data type. Depending on if it is a joint space or world space, the sub-type of the point differs. There is a point data type with two sub-types: '''JOINT''' and '''LOCATION'''. Both have a world space descriptor that additionally differentiates between the same sub-types. A world space coordinate is stored in a variable and is defined as: | ||
| + | |||
<pre> | <pre> | ||
DIM A AS LOCATION OF XYZR | DIM A AS LOCATION OF XYZR | ||
</pre> | </pre> | ||
| + | |||
The joint space is: | The joint space is: | ||
<pre> | <pre> | ||
DIM A AS JOINT OF XYZR | DIM A AS JOINT OF XYZR | ||
</pre> | </pre> | ||
| − | |||
| − | + | The point data type with its two sub-types (LOCATION and JOINT) and the world-space descriptor (XY, XYZ, XYZR, etc.) covers all the possible robot space variations. These variables are independent of the robot and can be used without having a robot defined in the system. When they are used in a connection with the robot or a group, the world-sub-types must be equal. | |
| + | |||
| + | The point can be manipulated as a numeric data type using all the arithmetic operations available (+-*/). The operations are defined as coordinate-by-coordinate operations. Only points of the same sub-type and same world-space can be combined. | ||
| + | |||
| + | Syntax used for point constants: a list of values separated by commands inside squared brackets ({}) denote points. If it is preceded by pound sign (#), it is a location: | ||
| − | |||
<pre> | <pre> | ||
DIM C AS LOCATION OF XYZR | DIM C AS LOCATION OF XYZR | ||
| − | C = #{0,0,0,0}DIM I AS JOINT OF XYZR | + | C = #{0,0,0,0} |
| + | |||
| + | DIM I AS JOINT OF XYZR | ||
I = {0,0,0,0} | I = {0,0,0,0} | ||
</pre> | </pre> | ||
| − | + | == User Units == | |
| + | |||
The softMC gives you the freedom to change and choose different units. Robot models have less flexibility. Due to a tight relation between joint and world-space, you must define joint position units in millimeters or degrees and all time units in seconds so both world space and joint space are compatible units. The units of world space are automatically set to millimeters-degrees-seconds. | The softMC gives you the freedom to change and choose different units. Robot models have less flexibility. Due to a tight relation between joint and world-space, you must define joint position units in millimeters or degrees and all time units in seconds so both world space and joint space are compatible units. The units of world space are automatically set to millimeters-degrees-seconds. | ||
| Line 69: | Line 96: | ||
In many robotics applications, mechanical construction introduced mechanical coupling between the axes. In such cases, two or more motors move only one joint. So activating only one motor causes motion in two axes (joints). There are many examples of such mechanical setups. Usually when the motors are dislocated for the joints, they are actuating. When the motor-actuating second joint is placed before the first joint, the second joint is moved by the motions of the first and second motors. Typical examples of such applications are displaced motors of a robotic arm (PUMA) moving the robot arm via chains or belts. Differential gearing on the last robot segment displaces the last motor (roll) from the end effector and both the fifth and sixth motors introduce motions on the sixth and with joint (Staubli RX series). | In many robotics applications, mechanical construction introduced mechanical coupling between the axes. In such cases, two or more motors move only one joint. So activating only one motor causes motion in two axes (joints). There are many examples of such mechanical setups. Usually when the motors are dislocated for the joints, they are actuating. When the motor-actuating second joint is placed before the first joint, the second joint is moved by the motions of the first and second motors. Typical examples of such applications are displaced motors of a robotic arm (PUMA) moving the robot arm via chains or belts. Differential gearing on the last robot segment displaces the last motor (roll) from the end effector and both the fifth and sixth motors introduce motions on the sixth and with joint (Staubli RX series). | ||
| − | Staubli RX – pair axes a5 ,a6: | + | |
| + | [[File:WRIST_CPLG.PNG |right]] | ||
| + | Staubli RX Wrist – pair axes a5 ,a6: | ||
<pre> | <pre> | ||
j6.pcmd = a6.pcmd – a5.pcmd | j6.pcmd = a6.pcmd – a5.pcmd | ||
| Line 97: | Line 126: | ||
Group joints are standard in the softMC firmware, covering coupling examples given above. | Group joints are standard in the softMC firmware, covering coupling examples given above. | ||
| − | + | == Motion Elements == | |
| − | The softMC is a multi-axis and multi-group system. In many aspects, groups and axes are the same. For example, both have properties like: '''AMAX''', '''VMAX''', '''VCRUISE'''. Another common aspect is the movement in both of them. '''MOVE''' moves both axes and groups. Although, there are motion commands that are group-only ('''CIRCLE''', '''MOVES''') or axis-only ('''JOG'''), when moving an axis separately, it is not possible to move the group containing the same axis and vice versa. The axis is active in a group. '''ATTACH''' and '''DETACH''' work the same way. You cannot attach an axis when its group is already attached. So, we can denote both axes and groups using one term, motion-element. | + | The softMC is a multi-axis and multi-group system. In many aspects, groups and axes are the same. For example, both have properties like: '''AMAX''', '''VMAX''', '''VCRUISE'''. Another common aspect is the movement in both of them. '''MOVE''' moves both axes and groups. Although, there are motion commands that are group-only ('''CIRCLE''', '''MOVES''') or axis-only ('''JOG'''), when moving an axis separately, it is not possible to move the group containing the same axis and vice versa. The axis is active in a group. '''ATTACH''' and '''DETACH''' work the same way. You cannot attach an axis when its group is already attached. So, we can denote both axes and groups using one term, '''motion-element'''. |
There are some properties that are axis- or group-only properties. For example '''DRIVEADDRESS''' is an axis-only property. | There are some properties that are axis- or group-only properties. For example '''DRIVEADDRESS''' is an axis-only property. | ||
| Line 135: | Line 164: | ||
Move-Joint simulates the behavior of moving a single axis by moving a single joint both by the parameters and physical motion. The only difference is that several motors are moving instead of just one. When moving joints, all motor limits within each group axis are checked. The joint movement is a group movement of one joint-coordinate with the group motion parameters copied from the shadow-axis. The following translation rule is true: | Move-Joint simulates the behavior of moving a single axis by moving a single joint both by the parameters and physical motion. The only difference is that several motors are moving instead of just one. When moving joints, all motor limits within each group axis are checked. The joint movement is a group movement of one joint-coordinate with the group motion parameters copied from the shadow-axis. The following translation rule is true: | ||
| + | |||
<pre> | <pre> | ||
| − | MOVE J1 10 | + | MOVE J1 10 <=> MOVE {10,0,0,0} abs = J1.abs vcruise = J1.vcruise acc = J1.acc |
| − | |||
| − | |||
</pre> | </pre> | ||
| − | |||
| − | |||
== Robot Models == | == Robot Models == | ||
| − | A robot is defined as a group with a special model type. | + | A robot is defined as a group with a special model type. (See the list of currently available robot models: [[Robot_Model_Table|'''robot_model_table''']]) |
| − | + | For example: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<pre> | <pre> | ||
| − | COMMON SHARED scara AS GROUP AxNm = a1 AxNm = a2 AxNm = a3 AxNm = a4 Model = 4 | + | COMMON SHARED scara AS GROUP AxNm = a1 AxNm = a2 AxNm = a3 AxNm = a4 Model = '''4''' |
</pre> | </pre> | ||
| + | === Robot Setup === | ||
| + | This automatically defines a robot with a SCARA kinematics model. Contrary to the regular groups that need only the axis to be enabled, you must set the robot parameters and configure them. The robot parameters needing to be set differ from robot to robot. For the SCARA robot, these are: | ||
| − | + | * Set all axes with all standard kinematics parameters. | |
| − | |||
| − | Set all axes with all standard kinematics parameters. | ||
| − | Define the roll-over properties. | + | * Define the roll-over properties. |
| − | Set all user-units factors for the entire group: '''VFAC''', '''AFAC''', '''JFAC''' | + | * Set all user-units factors for the entire group: '''VFAC''', '''AFAC''', '''JFAC''' |
| − | Set segment lengths and joints orientations for each robotic link. | + | * Set segment lengths and joints orientations for each robotic link. |
| − | Set kinematics of regular groups ('''VELOCITY''', '''ACCELERATION''', '''JERK''', etc.) | + | * Set kinematics of regular groups ('''VELOCITY''', '''ACCELERATION''', '''JERK''', etc.) |
| − | Set kinematics of Cartesian motions ('''VTRAN''','''VROT''', etc.) | + | * Set kinematics of Cartesian motions ('''VTRAN''','''VROT''', etc.) |
| − | Issue '''CONFIGGROUP''' | + | * Issue [[MC-Basic:CONFIGGROUP|'''CONFIGGROUP''']] |
Only after setting all these and successfully executing '''CONFIGGROUP''' can the robot be moved. Otherwise, an error is returned, stating that the group is not configured. The important difference between the regular groups (those with default model value 1) and the robot, is the necessity of executing '''CONFIGGROUP'''. In robot groups, no motion is allowed before the robot is configured. | Only after setting all these and successfully executing '''CONFIGGROUP''' can the robot be moved. Otherwise, an error is returned, stating that the group is not configured. The important difference between the regular groups (those with default model value 1) and the robot, is the necessity of executing '''CONFIGGROUP'''. In robot groups, no motion is allowed before the robot is configured. | ||
| − | Model value automatically defines the default robot world space descriptor. For model 4 (SCARA), the XYZR (x-y-z-roll) world-space is selected | + | Model value automatically defines the default robot world space descriptor. For model 4 (SCARA), the XYZR (x-y-z-roll) world-space is selected. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | In groups with the robot model defined (model > 1), the translation between joint- and world-space is | + | In groups with the robot model defined (model > 1), the translation between joint- and world-space is not simple. Translating joint coordinates into world coordinates is accomplished with '''TOCART''' taking both the robot and given joint coordinates (position variable) as input arguments. The output of this are world coordinates corresponding to the given joint position. |
The other direction is more complex. It is accomplished with '''TOJOINT''' receiving three input arguments: the robot, the given Cartesian point, and the configuration flag. | The other direction is more complex. It is accomplished with '''TOJOINT''' receiving three input arguments: the robot, the given Cartesian point, and the configuration flag. | ||
| Line 191: | Line 203: | ||
The configuration flag is used to select between the two translation functions. In most robot models, there is more than one joint coordinate description for the same world-space position. The different robot configurations can produce the same world-space positions with different joint-space values. The robot configurations differ from robot to robot. In SCARA, there are only two configurations: lefty (second joint coordinate is negative) and righty (second joint coordinate is positive). | The configuration flag is used to select between the two translation functions. In most robot models, there is more than one joint coordinate description for the same world-space position. The different robot configurations can produce the same world-space positions with different joint-space values. The robot configurations differ from robot to robot. In SCARA, there are only two configurations: lefty (second joint coordinate is negative) and righty (second joint coordinate is positive). | ||
| − | + | === Interpolation === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | For groups with robot models (model > 1), there is an additional moving type: [[MC-Basic:MOVES|'''MOVES''']]. The movement makes a straight path from the starting position to the given target position in the world space. The straightness is tightly-related to the working space. The same path can be straight in the Cartesian working space (XYZ) but curvy in joint space, and vice versa. '''MOVES '''is used solely for groups from type robot and cannot be used in regular groups. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | For groups with robot models (model > 1), there is an additional moving type: '''MOVES'''. The movement makes a straight path from the starting position to the given target position in the world space. The straightness is tightly-related to the working space. The same path can be straight in the Cartesian working space (XYZ) but curvy in joint space, and vice versa. '''MOVES '''is used solely for groups from type robot and cannot be used in regular groups. | ||
Straight line motion refers to motions that are straight lines in world-space. In groups with no robot model (model=1), all motions produced with '''MOVES''' are straight-line motions in joint-space. In regular linearly-dominant groups, most of their axes are linear. As the world-space and joint-space are identical, '''MOVES''' executes a straight line in both joint- and world-space. The target position can be given both in world- and joint-space coordinates. The movement differs from joint interpolation ('''MOVE'''). Instead of joint-space kinematics parameters used in regular groups, the world-space parameters for velocity, acceleration and jerk are used. These parameters are available in two forms:, one for the translational part of the motion and one for the rotational part (orientation). | Straight line motion refers to motions that are straight lines in world-space. In groups with no robot model (model=1), all motions produced with '''MOVES''' are straight-line motions in joint-space. In regular linearly-dominant groups, most of their axes are linear. As the world-space and joint-space are identical, '''MOVES''' executes a straight line in both joint- and world-space. The target position can be given both in world- and joint-space coordinates. The movement differs from joint interpolation ('''MOVE'''). Instead of joint-space kinematics parameters used in regular groups, the world-space parameters for velocity, acceleration and jerk are used. These parameters are available in two forms:, one for the translational part of the motion and one for the rotational part (orientation). | ||
| Line 218: | Line 213: | ||
The two sets of parameters define the straight line motion. Which parameter is dominant for the motion depends on the movement. If most of the movement is in translational position change and the orientation change is much smaller, the translational part is taken. Conversely, the rotational parameters define the movement. | The two sets of parameters define the straight line motion. Which parameter is dominant for the motion depends on the movement. If most of the movement is in translational position change and the orientation change is much smaller, the translational part is taken. Conversely, the rotational parameters define the movement. | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | [[Image:Axsystems;UserManual-1-Interpolation.png|caption|600px]]<br> | ||
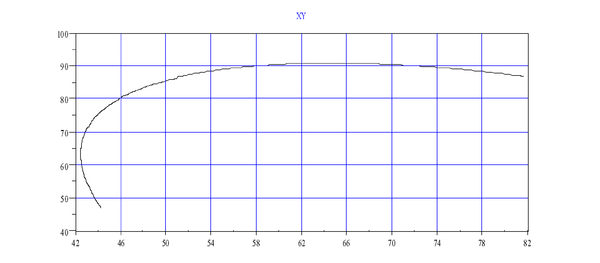
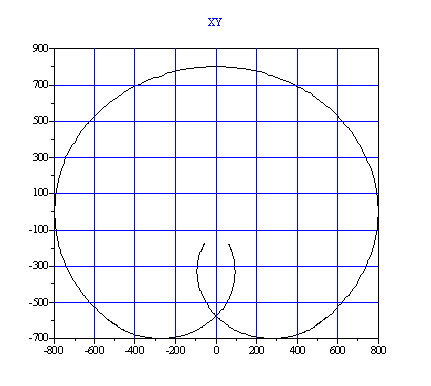
The following graph shows '''MOVES '''as seen in joint-space. | The following graph shows '''MOVES '''as seen in joint-space. | ||
| − | + | | | |
| − | [[Image:Axsystems;UserManual- | + | [[Image:Axsystems;UserManual-2-Interpolation.png|caption|600px]]<br> |
| − | |||
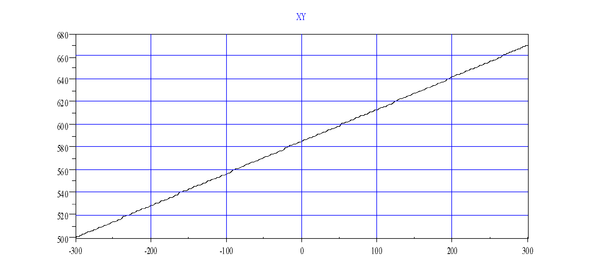
The following graph shows '''MOVES '''as seen in world-space. | The following graph shows '''MOVES '''as seen in world-space. | ||
| − | + | |- | |
| − | [[Image:Axsystems;UserManual- | + | | |
| − | + | [[Image:Axsystems;UserManual-3-Interpolation.png|caption|600px]]<br> | |
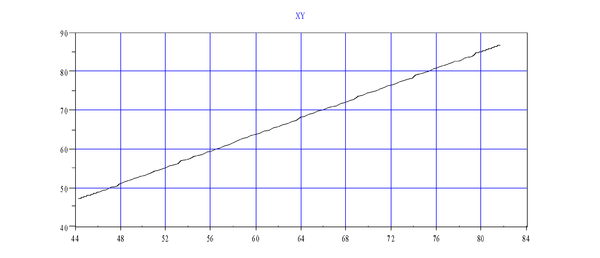
The following graph shows '''MOVE '''as seen in joint-space. | The following graph shows '''MOVE '''as seen in joint-space. | ||
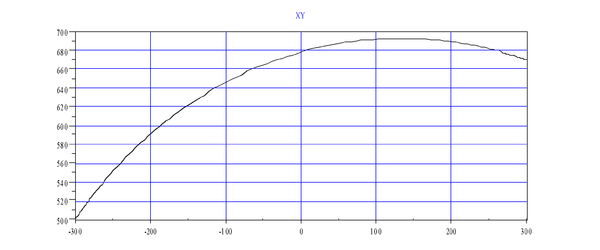
| + | | | ||
| + | [[Image:Axsystems;UserManual-4-Interpolation.png|caption|600px]]<br> | ||
| + | The following graph shows '''MOVES '''as seen in world-space. | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
There are four commands to make point-to-point movement in robot groups. There are two commands to interpolate the motion ('''MOVE''' and '''MOVES''') and two commands to define the target point ('''JOINT''' and '''LOCATION'''). The total combination of these gives four options. | There are four commands to make point-to-point movement in robot groups. There are two commands to interpolate the motion ('''MOVE''' and '''MOVES''') and two commands to define the target point ('''JOINT''' and '''LOCATION'''). The total combination of these gives four options. | ||
| Line 250: | Line 249: | ||
| style="border-top:0.018cm solid #000000;border-bottom:0.039cm double #000000;border-left:0.018cm solid #000000;border-right:none;padding-top:0cm;padding-bottom:0cm;padding-left:0.191cm;padding-right:0.191cm;"| MOVE <nowiki>#{400,400,0,0}</nowiki> | | style="border-top:0.018cm solid #000000;border-bottom:0.039cm double #000000;border-left:0.018cm solid #000000;border-right:none;padding-top:0cm;padding-bottom:0cm;padding-left:0.191cm;padding-right:0.191cm;"| MOVE <nowiki>#{400,400,0,0}</nowiki> | ||
| style="border-top:0.018cm solid #000000;border-bottom:0.039cm double #000000;border-left:0.018cm solid #000000;border-right:0.039cm double #000000;padding-top:0cm;padding-bottom:0cm;padding-left:0.191cm;padding-right:0.191cm;"| MOVE {45,45,0,0} | | style="border-top:0.018cm solid #000000;border-bottom:0.039cm double #000000;border-left:0.018cm solid #000000;border-right:0.039cm double #000000;padding-top:0cm;padding-bottom:0cm;padding-left:0.191cm;padding-right:0.191cm;"| MOVE {45,45,0,0} | ||
| − | |||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | === Contouring === | |
| − | |||
| − | |||
| − | |||
| − | == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Contouring connects different motions by defining the '''final velocity''' for each movement. This way, the motion does not stop at the segment. It is continued with the next motion. This method is applicable in one-axis applications, but has several drawbacks that become more prominent in multi-axis applications: | |
| − | + | * The angle between the movements' direction must be zero. Otherwise, a jump in velocity occurs. | |
| − | + | * It is not possible to connect arc with linear segments without a jump in acceleration. | |
| − | + | * You must calculate the achievable final velocities on each segment to stop after the last segment. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Working Envelope == | == Working Envelope == | ||
| Line 318: | Line 282: | ||
</pre> | </pre> | ||
| − | == Robot | + | |
| + | == Robot Configuration Flags == | ||
| + | |||
In robot models, there are several joint points representing the same robot end-effector position for each location point. To uniquely select between different joint coordinates, there are configuration flags. | In robot models, there are several joint points representing the same robot end-effector position for each location point. To uniquely select between different joint coordinates, there are configuration flags. | ||
For SCARA kinematics, there is only one configuration flag available: the arm flag. It indicates either lefty (1) (j2.pcmd > 0) or righty (2) (j2.pcmd > 0). A value of 1 (lefty) means that the joint coordinates having a positive second joint are taken to represent the given location. The current configuration of the robot is returned by '''ARMFBK'''. The value can be 1 or 2, depending on the position feedback value of the second joint. '''ARMFBK''' determines the movement's target position. It can be automatic (0), lefty(1) or righty(2). When a movement with a Cartesian target position is given, the joint coordinates of the target position are selected according to '''ARMFBK'''. If it is zero (automatic), the current robot configuration is used ('''ARMFBK'''). | For SCARA kinematics, there is only one configuration flag available: the arm flag. It indicates either lefty (1) (j2.pcmd > 0) or righty (2) (j2.pcmd > 0). A value of 1 (lefty) means that the joint coordinates having a positive second joint are taken to represent the given location. The current configuration of the robot is returned by '''ARMFBK'''. The value can be 1 or 2, depending on the position feedback value of the second joint. '''ARMFBK''' determines the movement's target position. It can be automatic (0), lefty(1) or righty(2). When a movement with a Cartesian target position is given, the joint coordinates of the target position are selected according to '''ARMFBK'''. If it is zero (automatic), the current robot configuration is used ('''ARMFBK'''). | ||
| − | PUMA models traditionally use three configuration flags (arm,elbow and wrist – ''' | + | PUMA models traditionally use three configuration flags (arm,elbow and wrist – '''[[MC-Basic:robot.ARMCMD|ARMCMD]]''', '''[[MC-Basic:robot.ELBOWCMD|ELBOWCMD]]''', '''[[MC-Basic:robot.WRISTCMD|WRISTCMD]]'''). |
| − | Another use of configuration flags is in the conversion function, '''TOJOINT'''. This function translates the given location point into joint point. It receives two arguments. The first is the location variable and the second is the configuration flag. | + | Another use of configuration flags is in the conversion function, '''[[MC-Basic:TOJOINT|TOJOINT]]'''. This function translates the given location point into joint point. It receives two arguments. The first is the location variable and the second is the configuration flag. |
= Points = | = Points = | ||
| − | A point is a | + | A point is a data type used for storing a list of doubles in a variable. The main advantage of points is that you can directly call the whole vector without having to access every element of it. There are two subt-ypes of the point data type: LOCATION and JOINT. Using both point types in the same expression results in a type mismatch translation error. Type casting between point types requires the usage of special system functions '''TOJOINT''' and '''TOCART'''. |
== Declaration == | == Declaration == | ||
| + | |||
A point must be declared before you can use it. The declaration of points is defined according to the type of robot (XYZR, XYZ, etc.). The softMC enables the declaration of point variables, which can be scalar or arrays. Point arrays may have up to 10 dimensions. Point variables are designed to hold a list of 2 to 10 double-type coordinates. A point variable is declared in relation to a robot type. Therefore, declaring a point variable must include the name of a valid robot type. The dimension of the point is the same as the dimension of the type of robot. The syntax is: | A point must be declared before you can use it. The declaration of points is defined according to the type of robot (XYZR, XYZ, etc.). The softMC enables the declaration of point variables, which can be scalar or arrays. Point arrays may have up to 10 dimensions. Point variables are designed to hold a list of 2 to 10 double-type coordinates. A point variable is declared in relation to a robot type. Therefore, declaring a point variable must include the name of a valid robot type. The dimension of the point is the same as the dimension of the type of robot. The syntax is: | ||
| Line 457: | Line 424: | ||
The point plus operator is used like any other data type. It adds each element of the first point with each element of the second point. The result is a point. | The point plus operator is used like any other data type. It adds each element of the first point with each element of the second point. The result is a point. | ||
<pre> | <pre> | ||
| − | ? | + | ?{1,2}+{2,4} |
| − | --> | + | --> {3,6} |
</pre> | </pre> | ||
| Line 464: | Line 431: | ||
The point minus operator is used like any other data type. It subtracts each element of the first point with each element of the second point. The result is a point. | The point minus operator is used like any other data type. It subtracts each element of the first point with each element of the second point. The result is a point. | ||
<pre> | <pre> | ||
| − | ? | + | ?{1,2}-{2,4} |
| − | --> | + | --> {-1,-2} |
</pre> | </pre> | ||
| Line 471: | Line 438: | ||
The point multiplication operator is used like any other data type. It multiplies each element of the first point with a number. You can only multiply a point with a single number (one-dimensional number). The result is a point. | The point multiplication operator is used like any other data type. It multiplies each element of the first point with a number. You can only multiply a point with a single number (one-dimensional number). The result is a point. | ||
<pre> | <pre> | ||
| − | ?2* | + | ?2*{2,4} |
| − | --> | + | --> {4,8} |
</pre> | </pre> | ||
| Line 478: | Line 445: | ||
The point division operator is used like any other data type. It divides each element of the first point with a number. You can only divide a point with a single number (one-dimensional number). The result is a point. | The point division operator is used like any other data type. It divides each element of the first point with a number. You can only divide a point with a single number (one-dimensional number). The result is a point. | ||
<pre> | <pre> | ||
| − | ? | + | ?{2,4}/2 |
| − | --> | + | --> {1,2} |
| − | ?2/ | + | ?2/{2,4} |
| − | --> | + | --> {1,0,5} |
</pre> | </pre> | ||
| Line 568: | Line 535: | ||
</pre> | </pre> | ||
| − | |||
| − | |||
== Point As An Expression == | == Point As An Expression == | ||
| − | + | Points properties can be stored as a point or can be compared as a point. For example: | |
<pre> | <pre> | ||
Dim A as Joint of XYZR | Dim A as Joint of XYZR | ||
| Line 589: | Line 554: | ||
</pre> | </pre> | ||
| − | Where for TOJOINT instruction the number and type of configuration flags depend on each robot type. Note that robot properties ARMCMD, ECMD, WCMD have all three values(0,1,2) where 0 is reserved for AUTO option. The configuration bits | + | Where for TOJOINT instruction the number and type of configuration flags depend on each robot type. Note that robot properties ARMCMD, ECMD, WCMD have all three values(0,1,2) where 0 is reserved for AUTO option. The configuration bits however have only two values (0,1). |
for SCARA robot : Arm ( Bit 0): value = 0 - Lefty(armcd = 1)value = 1- Righty(armcmd = 2) | for SCARA robot : Arm ( Bit 0): value = 0 - Lefty(armcd = 1)value = 1- Righty(armcmd = 2) | ||
| Line 599: | Line 564: | ||
Wrist ( Bit 2): value = 0 - Noflip (wcmd = 1) value = 1 - Flip (wcmd = 2) | Wrist ( Bit 2): value = 0 - Noflip (wcmd = 1) value = 1 - Flip (wcmd = 2) | ||
| − | for | + | for TRAVERSE-ARM robot: Arm ( Bit 0): value = 0 - Lefty(armcd = 1)value = 1 - Righty(armcmd = 2) |
| − | for DELTA, SCISSORS, … and other robots that have no configuration flags these | + | for DELTA, SCISSORS, … and other robots that have no configuration flags these fields are not used. |
The configuration flag argument of the tojoint is defined as: | The configuration flag argument of the tojoint is defined as: | ||
| Line 613: | Line 578: | ||
SAVE file = "Myfile.prg" type = all | SAVE file = "Myfile.prg" type = all | ||
LOAD Myfile.prg | LOAD Myfile.prg | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</pre> | </pre> | ||
= Refer to = | = Refer to = | ||
| − | * [[PUMA | + | * [[PUMA THETA Parameters|PUMA DH Parameters]] |
* [[SCARA J1 range|SCARA J1 Range]] | * [[SCARA J1 range|SCARA J1 Range]] | ||
* [[Speed_Picker_Y_Limit|Speed Picker Y Limit]] | * [[Speed_Picker_Y_Limit|Speed Picker Y Limit]] | ||
| − | * [[Kinematics | + | * [[Robot Kinematics Models|Kinematics Package]] |
[[Category:Motion Control|Kinematics]] | [[Category:Motion Control|Kinematics]] | ||
Latest revision as of 09:58, 24 April 2022
| Language: | English • 中文(简体) |
|---|
Contents
- 1 Introduction
- 2 Coupling
- 3 Points
- 4 Refer to
Introduction
Multiple axes can be combined into groups and moved. There are:
- simple groups (no models, can be either homogeneous or non-homogeneous)
- Cartesian groups (role of each axis is strictly defined, e.g.: XYZ, XYZR, ...)
- robots (the specific robot model is applied (SCARA, PUMA, ...)
Groups are data-objects (motion-elements) that enables us to move it's axes together synchronously. In case all axes are of same type (all linear or all rotary) their velocity, acceleration and jerk values can be combined (using a square root of the sum of squares) and the movement parameters will have physical meaning. We call these types of groups homogeneous groups.
Non-homogeneous groups consist of different axes, both rotary and linear. A feature was added to support the definition of velocities for non-homogeneous groups. In the setup, rotary and linear axes are declared. The system determines if it is a linear- or rotary-dominant group. For example, in SCARA robot, there are two rotary axes for the first and second joints and another rotary axis for the last joint (roll). There is only one linear axis (the Z axis). Such a system is rotary-dominant. Another example is the XYZ-Roll system. Here, there are two linear (X & Y) axes and another linear (Z axis) with just one rotary axis (roll). In this case, the system is linearly-dominant. Axis setup defines the group behavior. Each axis must be declared whether it is linear or rotary by setting POSITIONROLLOVERENABLE to either zero(0) for linear or one (1) for rotary.
In non-homogeneous groups, in joint-interpolated movements (MOVE) commanded velocity is always given according to the group dominance type (See: DOMINANCEMODE). If the group is linearly-dominant, the velocity (VCRUISE, VFINAL) is in linear units (mm/sec). The other non-linear axes are checked in the preparation phase of the movement. The velocity in these axes cannot exceed the maximum value. If it does, the overall (group) velocity is reduced.
There is only one exception to this rule. This is when a group movement is issued with only one axis in motion and all the others are stopped. Then, the given value of the velocity is taken directly in the units for that axis. For example, having movement on the third axis of the SCARA robot, the velocity value is in mm/sec.
The same is true for both acceleration and jerk values for group-interpolated motion.
In case the non-homogeneous group is improperly set, means there are axes of different types but the POSITIONROLLOVERENABLE of all of them is set to the same value, the group will still move but the velocity/acceleration/jerk values of the group will have non-physical meaning. In cases the numeric values between the axes differ significantly the system could behave wired.
| NOTE | |
| The above discussion is valid for simple joint-interpolated motion of a group only (See Move or Circle). Commands like Moves or Circle in Cartesian groups use Vtran and Vrot parameters |
Coordinate Systems
World coordinate system
Having different world and joint coordinates make the robot kinematics unique. The world coordinates are normally perceived as working coordinates of an application. Usually, there is some form of Cartesian coordinate system originating in the robot base.
Another set of coordinates is added for the orientation of the end-effector (gripper, etc.). The orientation of a body in space is normally described by three angles. Depending on the number of degrees of freedom (motors used to actuate the orientation joints), they could be unequal. The world space coordinates are given by its position part (X, XY or XYZ tupple), in most cases. In general, it could be anything from sphere coordinates to cylindrical system. The orientation component can use many forms for describing orientation. The mostly used coordinate system for orientation angles are the Euler angels: yaw, pitch and roll. Theoretically there are 12 different presentation of Euler angles, depending on the order of orientations in most robot models we are using the Z-Y-Z order.
Joint Coordinate system
The joint space of a robot is a relatively simple concept. A joint coordinate is a number uniquely describing the position of a robot segment relative to the previous robot segment. If the joint connecting the segment is rotary, the joint coordinates are in degrees of the rotation angle. If it is linear, the joint coordinates are the linear displacement (millimeters).
Point Data Type
The concept of joint coordinates is an n-tupple number. Each number represents the coordinate of the specific joint. The world coordinates are supported by different built-in types (XY, XYZ, XYZR) that describe each of the different world space representations. There can be different world space descriptions for the same (or same dimensional) world coordinates. Each robot has its default world-space type. Different robots could have same world space types, as long as they have same number of degrees of freedom (NDOF). For example, xy-table world space has XY world space descriptors. A SCARA robot having a Z axis for vertical motion and a roll axis for orientation uses world frame coordinates consisting of: X, Y, Z and roll or an XYZR descriptor.
The different coordinate systems are implemented as variables of different data types. Generally, a point in a coordinate system is defined as a point data type. Depending on if it is a joint space or world space, the sub-type of the point differs. There is a point data type with two sub-types: JOINT and LOCATION. Both have a world space descriptor that additionally differentiates between the same sub-types. A world space coordinate is stored in a variable and is defined as:
DIM A AS LOCATION OF XYZR
The joint space is:
DIM A AS JOINT OF XYZR
The point data type with its two sub-types (LOCATION and JOINT) and the world-space descriptor (XY, XYZ, XYZR, etc.) covers all the possible robot space variations. These variables are independent of the robot and can be used without having a robot defined in the system. When they are used in a connection with the robot or a group, the world-sub-types must be equal.
The point can be manipulated as a numeric data type using all the arithmetic operations available (+-*/). The operations are defined as coordinate-by-coordinate operations. Only points of the same sub-type and same world-space can be combined.
Syntax used for point constants: a list of values separated by commands inside squared brackets ({}) denote points. If it is preceded by pound sign (#), it is a location:
DIM C AS LOCATION OF XYZR
C = #{0,0,0,0}
DIM I AS JOINT OF XYZR
I = {0,0,0,0}
User Units
The softMC gives you the freedom to change and choose different units. Robot models have less flexibility. Due to a tight relation between joint and world-space, you must define joint position units in millimeters or degrees and all time units in seconds so both world space and joint space are compatible units. The units of world space are automatically set to millimeters-degrees-seconds.
Each axis has four scaling factors: PFAC,VFAC, AFAC, and JFAC. These translate encoder/resolver counts into user position units (inches, millimeters or revolutions). They also specify what time units are used in position derivations (VEL, ACC, JERK). As the position factor defines the ratio between counts and user position units, the rest of the factors define the ratio between milliseconds and user time units. Typically you have:
<axis>.pfac = <number of counts per user position units> <axis>.vfac = pfac/1000 (if in seconds) <axis>.afac = vfac/1000 (if in seconds) <axis>.jfac = afac/1000 (if in seconds)
Once all axes are set up, groups contain these axes. You must have the same user units on all axes. Set the group scaling factors. There is no position factor for the group! Instead, PFAC for each axis is used.
MOVE g1 {1,2,3} vcruise = 10
Target coordinates are given to each axis and translated into encoder/resolver counts using PFAC for each axis. VCRUISE is not related to any axis. Group factors, VFAC, AFAC, and JFAC are used. The group velocity is expressed in position user units per seconds.
To have system units properly working, set the unit factors (PFAC, VFAC, AFAC and JFAC) of each axis to millimeters-degrees-seconds and set group units to seconds:
<group>.vfac = 1/1000 <group>.afac = vfac/1000 <group>.jfac = afac/1000
Coupling
In many robotics applications, mechanical construction introduced mechanical coupling between the axes. In such cases, two or more motors move only one joint. So activating only one motor causes motion in two axes (joints). There are many examples of such mechanical setups. Usually when the motors are dislocated for the joints, they are actuating. When the motor-actuating second joint is placed before the first joint, the second joint is moved by the motions of the first and second motors. Typical examples of such applications are displaced motors of a robotic arm (PUMA) moving the robot arm via chains or belts. Differential gearing on the last robot segment displaces the last motor (roll) from the end effector and both the fifth and sixth motors introduce motions on the sixth and with joint (Staubli RX series).
Staubli RX Wrist – pair axes a5 ,a6:
j6.pcmd = a6.pcmd – a5.pcmd
BOSCH – SCARA – pair axes a3,a4:
j3.pcmd = a3.pcmd + 18.3*a4.pcmd.
PUMA – a2,a3 and a4:
j4.pcmd=a2.pcmd+a3.pcmd+a4.pcmd.
Scaling and Rotation:
j1 = 707.1*a1.pcmd + 707.1*a2.pcmd j2 = 707.1*a1.pcmd + 707.1*a2.pcmd
Orthogonal Correction:
j1 =10000*a1.pcmd j2 = 2.91*a1.pcmd + 10000*a2.pcmd
Group joints are standard in the softMC firmware, covering coupling examples given above.
Motion Elements
The softMC is a multi-axis and multi-group system. In many aspects, groups and axes are the same. For example, both have properties like: AMAX, VMAX, VCRUISE. Another common aspect is the movement in both of them. MOVE moves both axes and groups. Although, there are motion commands that are group-only (CIRCLE, MOVES) or axis-only (JOG), when moving an axis separately, it is not possible to move the group containing the same axis and vice versa. The axis is active in a group. ATTACH and DETACH work the same way. You cannot attach an axis when its group is already attached. So, we can denote both axes and groups using one term, motion-element.
There are some properties that are axis- or group-only properties. For example DRIVEADDRESS is an axis-only property.
MOVE consists two different command behaviors, Move-Group and Move-Axis. Move-Group moves the whole group together. All the axes within the group start and end the motion at the same time. Move-Group stays within the kinematics limits (VELOCITY, ACCELERATION, JERK) of the group and axes. The group limits are taken and imposed on the group motion (aggregate, space – XY, XYZ). The axis limits are imposed only proportionally to the ratio of the axis motion to the whole group motion. If axis X is moving halfway toward axis Y, only half the limit values are used. The total time of the motion is the time required for the slowest axis to accomplish the movement. Here, the slowest axis is the one with the largest path/velocity ratio and not necessary the axis with smallest maximum velocity (because if such an axis has no movement to make, it is not the slowest axis). On the other hand, Move-Axis checks only the limits of the specified axis and is independent of the limits of any group using this axis.
Profiler preparations can additionally reduce the motion parameter. This is typical for short movements where the given cruise velocity cannot be reached due to existing limitations of ACCELERATION and JERK.
Joints
Joints are virtual axes. Joints give the illusion of only one axis, both from the language point of view and looking at the physical movement of the coupled axis. The joint is analogous to an axis. Joints are denoted as J1, J2, etc.
Each joint actually represents one or several axes of the group, according to the given coupling matrix. If the group has no coupling matrix defined, the joint is a direct representation of the axis of the same ordinal number in the group as the joint index. To introduce another term, the "shadow-axis" of a joint is the axis with the same ordinal number in the group as the joint index. For example, if a group consists of axes A2, A3, A4, the shadow-axis of the joint J1 is A2.
Normally, all joint properties are a direct representation (have the same value) of shadow-axis properties, independent of whether the coupling matrix is defined or not. The only exceptions are properties related to joint position: PCMD, PFB, VCMD, VFB, CCMD, CFB, PMAX, and PMIN. These are unique for each joint.
Current positions and velocities are obtained according to the given coupling matrix. They are computed each time a query of these values is issued (PCMD, PFB, etc.). They are read-only and do not represent any specific internal variable. Symmetrically the same properties, when queried from a group (?g1.PCMD), return lists of joint-property values according to the coupling matrix. The movement’s target positions (MOVE or CIRCLE) of group movements are treated analogously (coupling matrix).
On the other hand, the joint’s position limits (PMAX and PMIN) are added to the joints. The position limit of the joint and the position limit of the shadow-axis are not related, but independent of whether the coupling matrix is defined or not. The joint position limits are always used when the coupling matrix is defined (COUPLED = 1). In this case, the shadow-axis limits are not used. This is only true for joint and group movements. Single-axis movement (e.g., MOVE A1 100) is limited only by the axis limits, independent of coupling.
Joints represent several axes of a group. Joint movements are actually group movements:
Move-Group = Move-Joint
Joint movement gives the illusion of moving one physical axis (MOVE J1 100), although several motors could be moving together. The movement is executed according to the specified joint’s movement parameters. For example:
A1.Acc = 100 MOVE A1 50
Is analogous to:
J1.Acc = 100 MOVE J1 50
Move-Joint simulates the behavior of moving a single axis by moving a single joint both by the parameters and physical motion. The only difference is that several motors are moving instead of just one. When moving joints, all motor limits within each group axis are checked. The joint movement is a group movement of one joint-coordinate with the group motion parameters copied from the shadow-axis. The following translation rule is true:
MOVE J1 10 <=> MOVE {10,0,0,0} abs = J1.abs vcruise = J1.vcruise acc = J1.acc
Robot Models
A robot is defined as a group with a special model type. (See the list of currently available robot models: robot_model_table)
For example:
COMMON SHARED scara AS GROUP AxNm = a1 AxNm = a2 AxNm = a3 AxNm = a4 Model = '''4'''
Robot Setup
This automatically defines a robot with a SCARA kinematics model. Contrary to the regular groups that need only the axis to be enabled, you must set the robot parameters and configure them. The robot parameters needing to be set differ from robot to robot. For the SCARA robot, these are:
- Set all axes with all standard kinematics parameters.
- Define the roll-over properties.
- Set all user-units factors for the entire group: VFAC, AFAC, JFAC
- Set segment lengths and joints orientations for each robotic link.
- Set kinematics of regular groups (VELOCITY, ACCELERATION, JERK, etc.)
- Set kinematics of Cartesian motions (VTRAN,VROT, etc.)
- Issue CONFIGGROUP
Only after setting all these and successfully executing CONFIGGROUP can the robot be moved. Otherwise, an error is returned, stating that the group is not configured. The important difference between the regular groups (those with default model value 1) and the robot, is the necessity of executing CONFIGGROUP. In robot groups, no motion is allowed before the robot is configured.
Model value automatically defines the default robot world space descriptor. For model 4 (SCARA), the XYZR (x-y-z-roll) world-space is selected.
In groups with the robot model defined (model > 1), the translation between joint- and world-space is not simple. Translating joint coordinates into world coordinates is accomplished with TOCART taking both the robot and given joint coordinates (position variable) as input arguments. The output of this are world coordinates corresponding to the given joint position.
The other direction is more complex. It is accomplished with TOJOINT receiving three input arguments: the robot, the given Cartesian point, and the configuration flag.
The configuration flag is used to select between the two translation functions. In most robot models, there is more than one joint coordinate description for the same world-space position. The different robot configurations can produce the same world-space positions with different joint-space values. The robot configurations differ from robot to robot. In SCARA, there are only two configurations: lefty (second joint coordinate is negative) and righty (second joint coordinate is positive).
Interpolation
For groups with robot models (model > 1), there is an additional moving type: MOVES. The movement makes a straight path from the starting position to the given target position in the world space. The straightness is tightly-related to the working space. The same path can be straight in the Cartesian working space (XYZ) but curvy in joint space, and vice versa. MOVES is used solely for groups from type robot and cannot be used in regular groups.
Straight line motion refers to motions that are straight lines in world-space. In groups with no robot model (model=1), all motions produced with MOVES are straight-line motions in joint-space. In regular linearly-dominant groups, most of their axes are linear. As the world-space and joint-space are identical, MOVES executes a straight line in both joint- and world-space. The target position can be given both in world- and joint-space coordinates. The movement differs from joint interpolation (MOVE). Instead of joint-space kinematics parameters used in regular groups, the world-space parameters for velocity, acceleration and jerk are used. These parameters are available in two forms:, one for the translational part of the motion and one for the rotational part (orientation).
When world-space has both position and orientation components, the straight-line motion includes interpolation on both position and orientation. Because these two are intrinsically different objects, two different parameters are needed: one for the translation (pure position interpolation): VELOCITYTRANS, ACCELERATIONTRANS, JERKTRANS; and one for the orientation (rotation interpolation): VELOCITYROT, ACCLERATIONROT, JERKROT. These parameter are used only for Cartesian interpolation (MOVES and CIRCLE). These parameters have no influence on joint interpolated motion (MOVE) because it is not a world-space interpolation.
The two sets of parameters define the straight line motion. Which parameter is dominant for the motion depends on the movement. If most of the movement is in translational position change and the orientation change is much smaller, the translational part is taken. Conversely, the rotational parameters define the movement.
There are four commands to make point-to-point movement in robot groups. There are two commands to interpolate the motion (MOVE and MOVES) and two commands to define the target point (JOINT and LOCATION). The total combination of these gives four options.
| LOCATION target | JOINT target | |
| Cartesian-Interpolation | MOVES #{400,400,0,0} | MOVES {45,45,0,0} |
| Joint-Interpolation | MOVE #{400,400,0,0} | MOVE {45,45,0,0} |
Contouring
Contouring connects different motions by defining the final velocity for each movement. This way, the motion does not stop at the segment. It is continued with the next motion. This method is applicable in one-axis applications, but has several drawbacks that become more prominent in multi-axis applications:
- The angle between the movements' direction must be zero. Otherwise, a jump in velocity occurs.
- It is not possible to connect arc with linear segments without a jump in acceleration.
- You must calculate the achievable final velocities on each segment to stop after the last segment.
Working Envelope
Robot working space is determined by the position limits of each joint. The working space (all reachable positions) is limited by the working envelope of the robot. From the outer side, it is limited by the arc made rotating the first joint with a fully stretched arm (j2.pcmd=0). This is the maximum radius of reachable points (RMAX). It is an internal value computed each time the robot is configured (CONFIGGROUP). Points given outside this radius are rejected with the error message, Point Too Far.
The other limit is the small circle with the radius (RMIN). This circle is obtained by rotating the first joint with a maximally-folded second joint (not more then 180 degrees). This radius is additionally enlarged by the robot's base size and the attached end-effector mechanism to prevent the robot from colliding with itself. The minimal working envelope radius (RMIN) is available to the user (contrary to RMAX). It is recommended that this value be set for each application according to the physical setup of the robot. If a point is given inside RMIN, an error message is returned. For example:
Program
attach
move {j1.pmin,j2.pmin,0,0}
while ismoving
sleep 1
End While
Print "Plotting the workspace"
move {j1.pmin,0,0,0}
move {j1.pmax,0,0,0}
move {j1.pmax,j2.pmax,0,0}
detach
End Program
Robot Configuration Flags
In robot models, there are several joint points representing the same robot end-effector position for each location point. To uniquely select between different joint coordinates, there are configuration flags.
For SCARA kinematics, there is only one configuration flag available: the arm flag. It indicates either lefty (1) (j2.pcmd > 0) or righty (2) (j2.pcmd > 0). A value of 1 (lefty) means that the joint coordinates having a positive second joint are taken to represent the given location. The current configuration of the robot is returned by ARMFBK. The value can be 1 or 2, depending on the position feedback value of the second joint. ARMFBK determines the movement's target position. It can be automatic (0), lefty(1) or righty(2). When a movement with a Cartesian target position is given, the joint coordinates of the target position are selected according to ARMFBK. If it is zero (automatic), the current robot configuration is used (ARMFBK).
PUMA models traditionally use three configuration flags (arm,elbow and wrist – ARMCMD, ELBOWCMD, WRISTCMD).
Another use of configuration flags is in the conversion function, TOJOINT. This function translates the given location point into joint point. It receives two arguments. The first is the location variable and the second is the configuration flag.
Points
A point is a data type used for storing a list of doubles in a variable. The main advantage of points is that you can directly call the whole vector without having to access every element of it. There are two subt-ypes of the point data type: LOCATION and JOINT. Using both point types in the same expression results in a type mismatch translation error. Type casting between point types requires the usage of special system functions TOJOINT and TOCART.
Declaration
A point must be declared before you can use it. The declaration of points is defined according to the type of robot (XYZR, XYZ, etc.). The softMC enables the declaration of point variables, which can be scalar or arrays. Point arrays may have up to 10 dimensions. Point variables are designed to hold a list of 2 to 10 double-type coordinates. A point variable is declared in relation to a robot type. Therefore, declaring a point variable must include the name of a valid robot type. The dimension of the point is the same as the dimension of the type of robot. The syntax is:
(COMMON SHARED|DIM {SHARED}) <variable_name> AS JOINT OF <robot_type>(COMMON SHARED|DIM {SHARED}) <variable_name> AS LOCATION OF <robot_type>
<robot_type> can be:
XYZR – Three cartesian axes + rollXY – two axes XY tableXYZ – three axes XYZ system
For example:
Common Shared JointXYZ As Joint Of XYZ Common Shared JointXYZR As Joint Of XYZR Common Shared LocXYZ As Location Of XYZ JointXYZ = LocXYZ --> Error – type mismatch
Variables
Two new variable types are defined for point variables in the translator: LOCATION and JOINT. For the translator, a point variable differs from any other type of variable (Long, Double, etc.) only by its type. A point variable is inserted to the expression tree as a variable leaf. The variable leaf retains data related to the point variable, including its context (system, program or local), its offset (taken from the symbol table), and its type (LOCATION or JOINT, also taken from the symbol table).
Declaration
When declaring a point variable, data corresponding to this variable is entered into the correct symbol table (depending on whether it is a system variable, a program variable, or a local variable). A point variable is defined in the symbol table by its name, its type (LOCATION or JOINT) and an offset of the data segment. Each offset of the data segment corresponds to the address of the point variable. The robot type string is sent to a special function that gives the robot-type value and the number of coordinates.
Constant Points
Constant points are location or joint vectors with an undefined robot type. The constant point’s subtype is defined by the shape of its brackets (#{ } for location, { } for joint). In the translator, each of these two vector types is considered an expression. Each expression-related command and manipulation (such as print commands, mathematical operators, etc.) can be applied for the joint and location vectors.
While executing a vector expression, each vector element is pushed separately into the stack as a double type expression (by executing the left side of the JOINT or LOCATION node). Long type vector elements are converted to double type expressions (in the coordinate node) after the execution of the expression at the right side of each coordinate node).
Execution of the right side of the JOINT or LOCATION node results in pushing the number of the vector elements into the stack (as a long type constant). The point’s subtype (determined by the shape of the vector’s brackets) is pushed to the stack (as a long type constant) by executing the third side of the JOINT/LOCATION node.
Vectors
Vectors are actually constant points, at which a list of 2 to 10 coordinates is written between curly brackets {}. In location vectors, the curly brackets are preceded by the # sign. A coordinate can be any type of expression (constant, variable, mathematical expression, function call, etc.) of long or double type. Long type coordinates are automatically converted to doubles. Unlike point variables, vectors are not related to robot types, and characterized merely by their size (number of coordinates).
{<expression_1>, …, <expression_n>} ‘ Joint vector
#{<expression_1>, …, <expression_n>} ‘ Location vector
Point variables and vectors appearing in the same expression must match in type (joint or location) and size.
Common Shared JointXYZ As Joint Of XYZ
JointXYZ = #{1.5, 2.8, 3} --> Error – type mismatch
PRINT {20, 6.7, 23} + #{8.43, 2, 0} --> Error – type mismatch
JointXYZ = {2, 6} --> Error – size mismatch
PRINT {20, 6.7, 23} - {5, 4, 22.9, 31} --> Error – size mismatch
Properties
Some group properties are points. There are several read-only properties of joint- (VELOCITYFEEDBACK, POSITIONCOMMAND, DEST_JOINT), and location-type (DEST, HERE, SETPOINT). There are also some location-type read-write properties, like TOOL, BASE, etc.
As in point variables, the robot type also characterizes point properties.Point properties appearing in expressions in a mixture with other points must match in type and robot type to point properties and variables, or in type and size to vectors.
Common Shared SCARA As Group Axnm = A1 Axnm = A2 Axnm = A3 Axnm = A4 Model = 4
Common Shared PointXYZR As Joint Of XYZR
Dim Shared PointXYZ As Joint Of XYZ
PointXYZR = SCARA.SetPoint --> Error – type mismatch (Setpoint returns a location)
PointXYZ = SCARA.VelocityFeedback --> Error – robot type mismatch
SCARA.Base = #{56.5, -104.7, -90.5} --> Error – size mismatch
Point Dimension
You do not define the size of the vector data type at the declaration of it, but you define the type of robot related to the point. This gives the point a dimension.
Point Assignment
Point assignment uses the following syntax:
<variable_name> = (<expr1>,<expr2>,<expr3>,…,<exprn>)() = #{} for location() = {} for joint
The expression can be a constant or other vector variable of the same robot type, but the size of the right side of the expression must equal the left side. If you try to assign a point with a point of other robot type, an error is received.
Single Coordinate Point Assignment
The syntax for assigning a single coordinate of a point is:
<variable_name>{<expression>} = <expression>
Point Query
The syntax for querying a point is:
?<variable_name>
Single Coordinate Point Query
The syntax for querying a single coordinate of a point:
?<variable_name>{<expression>}
Example 1
Common shared P1 as location of XYZR 'declaration of a vector (global)
P1 = #{1,2,3,4} 'assign the whole vector
P1 = #{1,2} 'return a translation error
?P1 'read the whole vector
?P1{2} 'read the second coordinate of the vector
Example 2
Common shared P2[5] as location XYZ 'declare a global array of vectors
P2[1] = #{1,2,3} 'assign the whole vector
P2[2] = #{5,2} 'return a translation error
?P2[1] 'read the whole vector
?P2[2]{2} 'read the second value of the vector
Operators
Like any other data type, you can use operators for points. The system only defines the equal operator (plus, minus, multiplication and division). Operations between points can only be performed between points of the same type and robot type (or size). All operations can also be performed between points and long or double type expressions.
Assignment
Point variables and read-write properties can be assigned by point variables, vectors and point properties compatible in type and size (or robot type).
Query
Point variables, properties and vectors return a value, so they can all be queried through printing or assignment into a compatible point variable or read-write property.
Common Shared SCARA As Group Axnm = A1 Axnm = A2 Axnm = A3 Axnm = A4 Model = 4
Common Shared PointVar1 As Joint Of XYZR
Dim Shared PointVar2 As Joint Of XYZ
Dim PointArr[4] As Joint Of XYZR
PointVar1 = PointArr[2]
PointVar2 = {23.4, 60, 42}
PointArr[1] = SCARA.PositionCommand
SCARA.Tool = #{10, 20,30, 0}
PRINT PointVar2, SCARA.Tool, {100.3, 20}
--> {23.4 , 60 , 42} #{10 , 20 , 30 , 0} {100.3 , 20}
Plus
The point plus operator is used like any other data type. It adds each element of the first point with each element of the second point. The result is a point.
?{1,2}+{2,4}
--> {3,6}
Minus
The point minus operator is used like any other data type. It subtracts each element of the first point with each element of the second point. The result is a point.
?{1,2}-{2,4}
--> {-1,-2}
Multiplication
The point multiplication operator is used like any other data type. It multiplies each element of the first point with a number. You can only multiply a point with a single number (one-dimensional number). The result is a point.
?2*{2,4}
--> {4,8}
Division
The point division operator is used like any other data type. It divides each element of the first point with a number. You can only divide a point with a single number (one-dimensional number). The result is a point.
?{2,4}/2
--> {1,2}
?2/{2,4}
--> {1,0,5}
Compound (:)
Is an operator specific for points, which should be operated between two locations of the same size (or robot type).
? #{-56.5 , -104.7 , 89.5} : #{ 0.0, -104.7 , -0.5}
--> #{-56.5 , -209.4 , 89}
Limitations
MOD (modulus), ^ (power), logic and bitwise operators cannot be used for points.
Points cannot be used as condition in flow control statements and event definitions.
Points cannot be recorded.
Points in Functions
Point variables can be passed to functions and subroutines both by reference and by value. An entire array of points can also be passed (by reference) to a function or subroutine. On the other hand, point properties and vectors can only be passed by value. Points can also serve as return values of functions. However, the point type and size (or robot type) of an argument or a return value must match function declaration.
Passing By Value And Reference
A point can be passed by value and by reference like any other data type. For example:
Program
Dim p1 as joint of XYZR
Call Sub1(P1)
?p1
End program
Sub Sub1(X as joint of XYZR)
X = {1,2,3,4}
End Sub
This program assigns P1 to {1, 2, 3, 4} and prints {1, 2, 3, 4} as output. When a point is passed by reference or value, you can only pass a point of the same robot type to X. Otherwise, you receive a translation error.
Example 1
Program
Dim p1 as location of XYZR
Call Sub1(P1 --> TRANSLATION ERROR !!!
?p1
End program
Sub Sub1(X as location of XYZ)
X = #{1,2,3,4}
End Sub
Example 2
Program
Dim p1 as joint of XYZR
Call Sub1(P1) --> TRANSLATION ERROR !!!
?p1
End program
Sub Sub1 (ByVal X as joint of XYZ)
X = {1,2,3,4}
End Sub
Returning Point From Function
A function can return a point variable like any other data type. For example:
Dim A as location of XYZR
Program
Move G1 MyFunc(1) vcruise=299
--> this will be OK if G1 is of XYZR robot type.
End Program
Function MyFunc(i1 as long) as location of XYZR
MyFunc = #{1,2,3,4}
End Function
Motion Commands
Some motion commands use point nodal parameters when applied on groups. For example: CIRCLE, MOVE and MOVES.
Some nodal parameters can be assigned with both point types (LOCATION and JOINT), like CIRCLECENTER, CIRCLEPOINT and the target positions of MOVE and MOVES. Other nodal parameters can accept only location points, like TOOL, BASE, etc. Assign all nodal parameters with points compatible in robot type or size to the group.
Common Shared SCARA As Group Axnm = A1 Axnm = A2 Axnm = A3 Axnm = A4 Model = 4
Common Shared JointXYZ As Joint Of XYZ
MOVE SCARA JointXYZ --> Error – robot type mismatch
CIRCLE SCARA Angle = 180 CircleCenter = #{350, 500, -80}
--> Error – size mismatch
MOVES SCARA #{-22, 503.8, -8.3, 149} Base = SCARA.Dest_Joint
--> Error – type mismatch
Point As An Expression
Points properties can be stored as a point or can be compared as a point. For example:
Dim A as Joint of XYZR
A = {1,2,3,4}
A = G1.Pcmd
A = G2.Pcmd --> returns a translation error if G2 is not of XYZR type.
Functions
The following functions are defined:
<XYZR location> = TOCart (<group>, <XYZR JOINT>) <XYZR Joint> = ToJoint(<group>,<XYZR LOCATION>,<configuration-flag:integer>) <double> distl(<location>,<location>) Distance between points (length). <double> distr(<location>,<location>) Distance between points (angle).
Where for TOJOINT instruction the number and type of configuration flags depend on each robot type. Note that robot properties ARMCMD, ECMD, WCMD have all three values(0,1,2) where 0 is reserved for AUTO option. The configuration bits however have only two values (0,1).
for SCARA robot : Arm ( Bit 0): value = 0 - Lefty(armcd = 1)value = 1- Righty(armcmd = 2)
for PUMA robot : Arm ( Bit 0): value = 0 - Lefty(armcd = 1) value = 1 - Righty(armcmd = 2)
Elbow ( Bit 1):value = 0 - Below(ecmd = 1) value = 1 - Above(ecmd = 2)
Wrist ( Bit 2): value = 0 - Noflip (wcmd = 1) value = 1 - Flip (wcmd = 2)
for TRAVERSE-ARM robot: Arm ( Bit 0): value = 0 - Lefty(armcd = 1)value = 1 - Righty(armcmd = 2)
for DELTA, SCISSORS, … and other robots that have no configuration flags these fields are not used.
The configuration flag argument of the tojoint is defined as:
SAVE/LOAD
Each global variable can be stored in a file. The variable and its value are stored in same syntax as it is defined in the program. You can select a data-type to be stored. If a data-type is selected, the SAVE command stores only global variables of that data type. If file with same name already exist its extension is renamed to *.bak and new file is created. Loading the file overwrites the values of the saved global variables. You can save all the points related to some type of robot. For example:
SAVE file = "Myfile.prg" type = location robottype = xyzr SAVE file = "Myfile.prg" type = all LOAD Myfile.prg