Difference between revisions of "Galileo Sphere Robot (GSR) Kinematics/zh-hans"

From SoftMC-Wiki
Jump to: navigation, search
(Created page with "{{Languages}} =Robot Kinematics for Galileo Sphere Robot= Image:GSR-SETUP.JPG 400px 400px ==Robot Defi...")
 
 
Line 1: Line 1:
−
{{Languages}}
+
{{Languages|Galileo_Sphere_Robot_(GSR)_Kinematics}}
−
=Robot Kinematics for Galileo Sphere Robot=
+
=伽利略球机器人的机器人运动学=
  
 
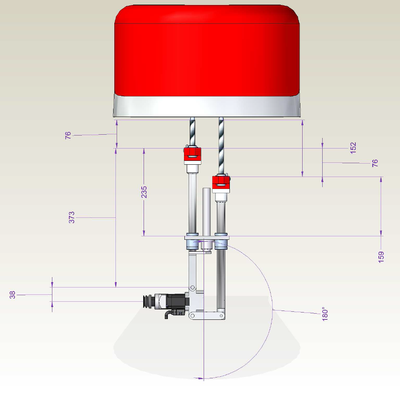
[[Image:GSR-SETUP.JPG]]  [[Image:GSR-SIDE-DRAWINGS.PNG|400px]]  [[Image:GSR-FRONT-DRAWING.PNG|400px]]
 
[[Image:GSR-SETUP.JPG]]  [[Image:GSR-SIDE-DRAWINGS.PNG|400px]]  [[Image:GSR-FRONT-DRAWING.PNG|400px]]
  
  
−
==Robot Definition as a Group of Axes with a Predefined Point Type==
+
==机器人定义为具有预定义点类型的一组轴==
  
−
The robot kinematics will be assigned to a new model type ('''15''') with a '''XYZPR''' (x,y,z, pitch, roll) point type. The following line defines the GALILEO robot as a new system variable:
+
机器人运动学将被分配到具有'''XYZPR'''（x，y，z，pitch，roll）点类型的新模型类型（'''15'''）。 以下行将GALILEO机器人定义为新的系统变量:
 
<pre>
 
<pre>
 
Common Shared GALILEO As Group Axnm = A1 Axnm = A2 Axnm = A3 Axnm = A4  Axnm = A5 model = 15 of '''xyzpr'''
 
Common Shared GALILEO As Group Axnm = A1 Axnm = A2 Axnm = A3 Axnm = A4  Axnm = A5 model = 15 of '''xyzpr'''
 
</pre>
 
</pre>
  
−
==Kinematics of the Robot ==
+
==机器人运动学 ==
  
 
[[Image:GSR0.PNG|400px]]
 
[[Image:GSR0.PNG|400px]]
  
−
===Joint Coordinates===
+
===关节坐标系===
  
 
{| border = 1
 
{| border = 1
Line 32: Line 32:
 
|}
 
|}
  
−
'''Three Rotary Axes:'''
+
'''三个旋转轴:'''
−
* theta1 – big horizontal rotary (J1 or joint #1)
+
* theta1 – 大水平旋转 (J1 或 joint #1)
−
* theta2 – pitch axis (J2 or joint #2)
+
* theta2 – 俯仰轴(J2 或 joint #2)
−
* theta3 – tool rotation (J5 or joint #5)
+
* theta3 – 工具旋转 (J5 或 joint #5)
  
−
'''Two linear axes:'''
+
'''两个线性轴:'''
−
* Z1 (J3 or joint #3)
+
* Z1 (J3 或 joint #3)
−
* Z2 (J4 or joint #4)
+
* Z2 (J4 或 joint #4)
  
  
−
The Z1 is the linear axis without connecting rod.
+
Z1是无连杆的线性轴。
−
General presentation of the robot joint point in MC-Basic language is (list of numeric expressions inside curly brackets):
+
MC-Basic语言中机器人关节点的一般介绍是（大括号内的数值表达式）:
−
 
 
 
<pre>{J1, J2, J3, J4, J5}</pre>
 
<pre>{J1, J2, J3, J4, J5}</pre>
  
−
===Cartesian Coordinates===
+
===笛卡尔坐标系===
  
−
Cartesian coordinates (world) of the robot TCP (Tool Center Point) are (Xw, Yw, Zw). Orientation of the robot tool’s Z axis is always expressed as a rotation needed to rotate the Z world (Zw) axis into Z tool (Zt) axis. It can be expressed with 3 Euler angles (Yaw, Pitch, Roll) of the ZYZ order of rotations.
+
机器人TCP（工具中心点）的笛卡尔坐标（世界）是（Xw，Yw，Zw）。 机器人工具Z轴的姿态总是表示为将Z世界（Zw）轴旋转到Z刀具（Zt）轴所需的旋转。 它可以用ZYZ旋转次数的3欧拉角（Yaw，Pitch，Roll）表示。
 
'''Yaw Angle:'''
 
'''Yaw Angle:'''
−
Rotating (Xw, Yw, Zw) system around Zw axis into (X1, Y1, Z1)
+
绕Zw轴旋转（Xw，Yw，Zw）到（X1，Y1，Z1）
 
'''Pitch Angle:'''
 
'''Pitch Angle:'''
−
Rotating (X1, Y1, Z1) system around Y1  axis into (X2, Y2, Z2)
+
绕Y1轴旋转（X1，Y1，Z1）到（X2，Y2，Z2）
 
'''Roll Angle:'''
 
'''Roll Angle:'''
−
Rotating (X2, Y2, Z2) system around Z2  axis into (X3, Y3, Z3) which coincides to (Xt, Yt, Zt)
+
绕轴Z2（X2，Y2，Z2）系统到（X3，Y3，Z3），与（XT，YT，ZT）重合
  
−
As the given robot has only 5 degrees of freedom (DOF) we are reducing the orientation representation to Pitch and Roll angles only. That corresponds to rotations around Y2 (axis obtained after rotating Yw with θ1) and Z3 tools Z axis (in that order).
+
由于给定的机器人只有5个自由度（DOF），所以我们只将姿态表示法减少到俯仰和翻滚角度。 这对应于绕Y2的旋转（旋转Yw与θ1之后获得的轴）和Z3工具Z轴（依次）。
  
−
General presentation of the robot Cartesian point in MC-Basic language is  (list of numeric expressions inside curly brackets preceded with hash sign):
+
一般在MC-Basic语言中的介绍机器人笛卡尔点是（带哈希符号之前的大括号内的数值表达式列表）:
  
 
<pre>#{X, Y, Z, Pitch, Roll}</pre>
 
<pre>#{X, Y, Z, Pitch, Roll}</pre>
  
−
=Geometry=
+
=几何形状=
  
−
The important geometrical parameters of the robot are:
+
机器人的重要几何参数是:
  
 
[[Image:GSR1.PNG|400px]]
 
[[Image:GSR1.PNG|400px]]
  
−
List of parameters:
+
参数列表:
 
{| border = 1
 
{| border = 1
−
|Name||Units||Description||MC-Basic property
+
|名称||单位||描述||MC-Basic 属性
 
|-
 
|-
 
|D1||mm||Distance between the axes||<robot>.Link[1][1]
 
|D1||mm||Distance between the axes||<robot>.Link[1][1]
 
|-
 
|-
−
|D2||mm||Tool mounting rod||<robot>.Link[1][2]
+
|D2||mm||工具安装杆||<robot>.Link[1][2]
 
|-
 
|-
−
|D3||mm||Extension rod||<robot>.Link[1][3]
+
|D3||mm||延长杆||<robot>.Link[1][3]
 
|-
 
|-
−
|L1||mm||Tool Length||<robot>.Link[2][1]
+
|L1||mm||工具长度||<robot>.Link[2][1]
 
|-
 
|-
−
|B1||mm||Vertical (Z) offset of the θ2 rotation center (C2) from the center of θ1-circle (C1).||<robot>.Link[2][2]
+
|B1||mm||θ2旋转中心（C2）与θ1圆（C1）中心的垂直（Z）偏移。||<robot>.Link[2][2]
 
|}
 
|}
  
−
There are two additional parameters that are defined implicitly by defining the zero coordinate
+
通过定义z轴（z1off和z2off）的零坐标，隐含定义了两个附加参数。两个z轴在同一行应为零（见图）。 这两个将包括从轴编码器零位置到θ2的旋转轴的偏移 - 包括连接到它的所有固定的附加联轴器（在图中未示出，因为它们不交替基本机器人运动学）。
−
of the z axes (z1off and z2off). Both z axes should have zero at same line (see picture). These two will include the offset from the axis encoder zero position to the rotation axis of θ2  - including all fixed additional linkages connected to it (not depicted in the picture as they do not alternate the basic robot kinematics).
 
  
−
{{Note/Important|The assumption is that the robot has symmetrical setup. The tool flange is in the middle of D2 link and the center of rotation of the theta2 is in the middle of the theta1 circle. It is crucial to have these two requirements fulfilled, if not the kinematics relations will be invalid.
+
{{Note/Important|假设机器人具有对称的设置。 工具法兰在D2连杆的中间，theta2的旋转中心位于θ1圆的中间。 要达到这两项要求至关重要，否则运动学关系无效。
 
}}
 
}}
  
−
=Singularities=
+
=奇异点=
  
−
Theoretically speaking there are two singularities of these kinematics, let’s call them roll-singularity and linkage-singularity (these names are just arbitrarily given as we need somehow to denote them), but we will handle just one and the other will be not available to the user. Here is the explanation:
+
理论上说，这些运动学有两个奇点，我们称之为滚动奇异性和连杆奇异性（这些名称只是随意地给出，因为我们需要以某种方式表示它们），但是我们将只处理一个，而另一个对用户将不可用。以下为解释:
  
−
==Roll-singularity==
+
==旋转奇异点==
  
  
 
[[Image:GSR-CONFIG.PNG|400px]]
 
[[Image:GSR-CONFIG.PNG|400px]]
  
−
This type of singularity happens when θ<sub>1</sub> and θ<sub>3</sub> are co-linear. Their sum (θ<sub>1</sub> + θ<sub>3</sub>) builds the Cartesian roll angle and any combination of these two numbers will represent the same roll angle.
+
当θ<sub>1</sub>和θ<sub>3</sub>都是共线的时，发生这种奇异性。 它们的和(θ<sub>1</sub> + θ<sub>3</sub>)构建笛卡尔转角，并且这两个数字的任何组合将代表相同的转角。
 +
 
  
−
==Linkage-singularity==
+
==连杆奇异==
  
 
[[Image:GSR-RSING.PNG|400px]]
 
[[Image:GSR-RSING.PNG|400px]]
  
−
It is a typical four-bar mechanism singularity where for the same position of Z1X segment there are two solutions for Z2 point.  In order to avoid problems with this type of singularity only solutions with minimal x angle will be taken (x’ angle in the drawing).
+
这是一个典型的四杆机构奇异性，对于Z1X段的相同位置，Z2点有两个解决方案。 为了避免这种奇异点的问题，只能采取最小x角的解决方案（图中的x'角）。
 
 
 
 
  
−
=Configuration Flags=
+
=配置标志=
  
−
Actually there should be two configuration flags in the system. But, as the one of the configuration is not allowed, only one (ARM) is made available (accessible for reading and writing) to the user.
+
实际上系统中应该有两个配置标志。 但是，由于其中的一个配置不允许，所以只有一个（ARM）用户可用（用于读取和写入）。
  
 
[[Image:GSR-LSING.PNG|400px]]
 
[[Image:GSR-LSING.PNG|400px]]
  
−
The Arm configuration flag is defined according to the following reasoning:<br>
+
Arm配置标志根据以下定义:<br>
  
−
If the tool-tip is on the same side as the θ<sub>2</sub> slider it is '''RIGHTY'''; otherwise it is '''LEFTY'''
+
如果工具尖端与θ<2>滑块位于同一侧，则为“RIGHTY”。 否则是“'LEFTY'''
  
−
Or:<br>
+
或:<br>
  
−
Arm is '''LEFTY''' if r > 0<br>
+
如果 r > 0，Arm 为'''LEFTY'''<br>
−
Arm is '''RIGHTY''' if r < 0
+
如果r<0,Arm is '''RIGHTY'''
  
 +
在MC-Basic语言中:<br>
  
−
In the MC-Basic language it is:<br>
+
* [[MC-Basic:robot.ARMCMD|<robot>.Acmd]]为命令配置
 +
* [[MC-Basic:robot.ARMFBK|<robo>.Afbk]]当前（反馈）配置
  
−
* [[MC-Basic:robot.ARMCMD|<robot>.Acmd]]  for the commanded configuration
 
−
* [[MC-Basic:robot.ARMFBK|<robo>.Afbk]] for the current(feedback) configuration
 
  
−
=Typical Robot Poses=
+
=典型的机器人姿态=
−
Here is a list of some typical poses for a better understanding of the workspace coordinates. They do not necessary represent the feasible positions of the robot (due to some axis position limitations) but they are good examples to finalize and test robot kinematics definitions.
+
以下列出了一些更好地了解工作空间坐标的典型姿势。 它们不需要代表机器人的可行位置（由于某些轴位置限制），但它们是完成和测试机器人运动学定义的好例子。
  
 
[[Image:GSR-POS0.PNG|400px]]
 
[[Image:GSR-POS0.PNG|400px]]
  
−
• Horizontal position, pitch angle = 90 degrees:
+
• 水平位置，俯仰角= 90度:
 
{0,0,Z1,Z2-D3,0}  #{Z1+L1,B1,-90,0}
 
{0,0,Z1,Z2-D3,0}  #{Z1+L1,B1,-90,0}
  
−
• Same pose rotating theta 3 – directly translated into roll angle.
+
• 相同姿态旋转θ3 - 直接转换成旋转角度
 
{0,0,Z1,Z2-D3,45}  #{Z1+L1,B1,-90,45}
 
{0,0,Z1,Z2-D3,45}  #{Z1+L1,B1,-90,45}
 
{0,0,Z1,Z2-D3,-45}  #{Z1+L1,B1,-90,-45}
 
{0,0,Z1,Z2-D3,-45}  #{Z1+L1,B1,-90,-45}
Line 145: Line 144:
  
  
−
Horizontal position, pitch angle = ±90 degrees:
+
水平位置，俯仰角= ±90度:
 
{90,0,Z1,Z1-D3,0}  #{0,-(Z1+L1),B1,-90,0}
 
{90,0,Z1,Z1-D3,0}  #{0,-(Z1+L1),B1,-90,0}
 
{-90,0,Z1,Z1-D3,0}  #{0,+(Z1+L1),B1,-90,0}
 
{-90,0,Z1,Z1-D3,0}  #{0,+(Z1+L1),B1,-90,0}
Line 151: Line 150:
 
[[Image:GSR-POS2.PNG|400px]]
 
[[Image:GSR-POS2.PNG|400px]]
  
−
• Singular point:
+
• 奇异点:
 
{0,90,Z1,Z1-D3,0}  #{0,0,B1+(Z1+L1),0,0}  
 
{0,90,Z1,Z1-D3,0}  #{0,0,B1+(Z1+L1),0,0}  
 
{R,90,Z1,Z1-D3,-R}  #{0,0, B1+ (Z1+L1),0,0}  for any R!
 
{R,90,Z1,Z1-D3,-R}  #{0,0, B1+ (Z1+L1),0,0}  for any R!
Line 247: Line 246:
  
  
−
{{Note|At this point we have the linkage singularity.}}
+
{{Note|在这一点上，我们有连杆奇异点}}

Latest revision as of 08:15, 29 May 2017

语言: English  • 中文（简体）‎

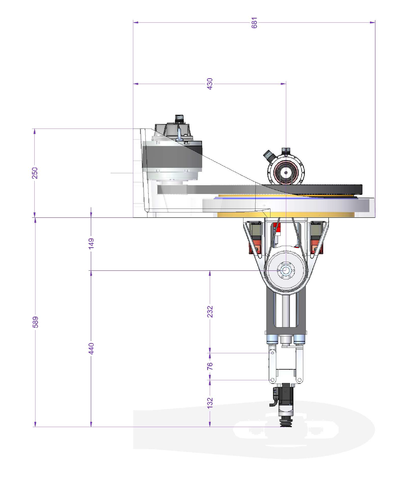
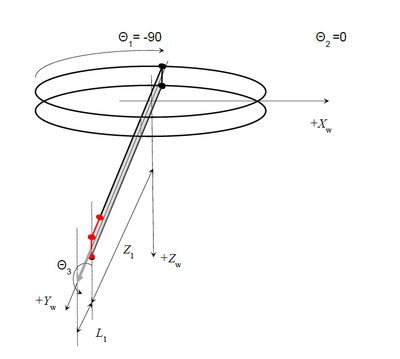
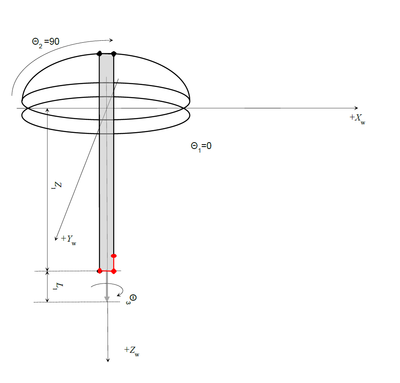
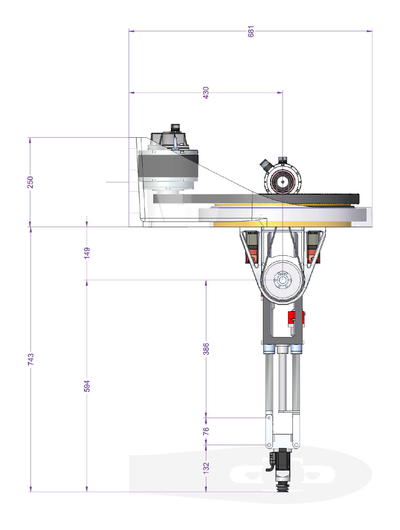
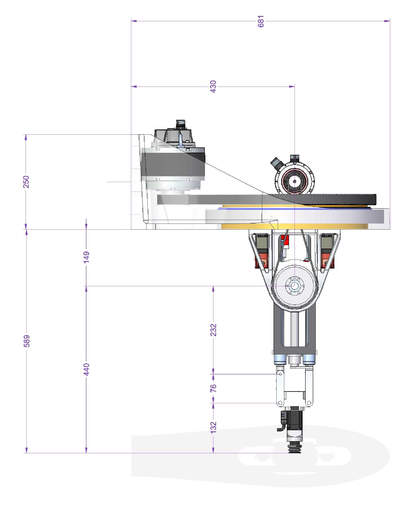
伽利略球机器人的机器人运动学

GSR-SETUP.JPG GSR-SIDE-DRAWINGS.PNG GSR-FRONT-DRAWING.PNG


机器人定义为具有预定义点类型的一组轴

机器人运动学将被分配到具有XYZPR（x，y，z，pitch，roll）点类型的新模型类型（15）。 以下行将GALILEO机器人定义为新的系统变量: 

Common Shared GALILEO As Group Axnm = A1 Axnm = A2 Axnm = A3 Axnm = A4  Axnm = A5 model = 15 of '''xyzpr'''

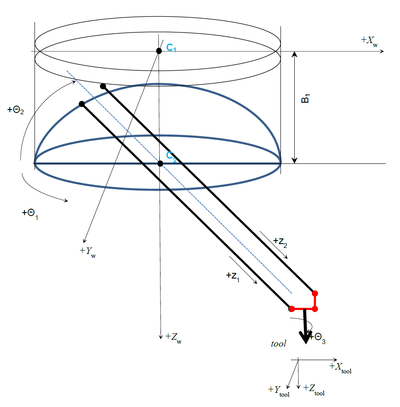
机器人运动学

GSR0.PNG

关节坐标系

Axis name Joint Type Range Units
Theta1 J1 Rotary axis [-180,180] deg
Theta2 J2 Rotary axis [-10,90] deg
Z1 J3 Linear [Z1min,Z1max] mm
Z2 J4 Linear [Z2min,Z2max] mm
Theta3 J5 Rotary axis Multi turn deg

三个旋转轴:

  • theta1 – 大水平旋转 (J1 或 joint #1)
  • theta2 – 俯仰轴(J2 或 joint #2)
  • theta3 – 工具旋转 (J5 或 joint #5)

两个线性轴:

  • Z1 (J3 或 joint #3)
  • Z2 (J4 或 joint #4)


Z1是无连杆的线性轴。 MC-Basic语言中机器人关节点的一般介绍是（大括号内的数值表达式）: 

{J1, J2, J3, J4, J5}

笛卡尔坐标系

机器人TCP（工具中心点）的笛卡尔坐标（世界）是（Xw，Yw，Zw）。 机器人工具Z轴的姿态总是表示为将Z世界（Zw）轴旋转到Z刀具（Zt）轴所需的旋转。 它可以用ZYZ旋转次数的3欧拉角（Yaw，Pitch，Roll）表示。 Yaw Angle: 绕Zw轴旋转（Xw，Yw，Zw）到（X1，Y1，Z1） Pitch Angle: 绕Y1轴旋转（X1，Y1，Z1）到（X2，Y2，Z2） Roll Angle: 绕轴Z2（X2，Y2，Z2）系统到（X3，Y3，Z3），与（XT，YT，ZT）重合

由于给定的机器人只有5个自由度（DOF），所以我们只将姿态表示法减少到俯仰和翻滚角度。 这对应于绕Y2的旋转（旋转Yw与θ1之后获得的轴）和Z3工具Z轴（依次）。

一般在MC-Basic语言中的介绍机器人笛卡尔点是（带哈希符号之前的大括号内的数值表达式列表）: 

#{X, Y, Z, Pitch, Roll}

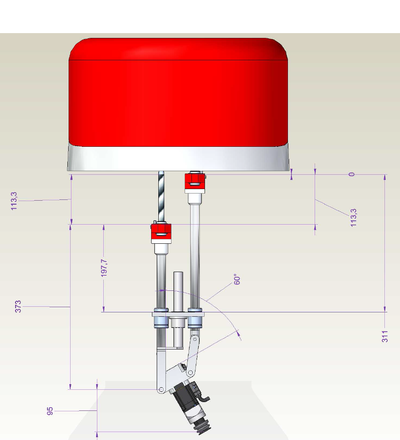
几何形状

机器人的重要几何参数是:

GSR1.PNG

参数列表:

名称 单位 描述 MC-Basic 属性
D1 mm Distance between the axes <robot>.Link[1][1]
D2 mm 工具安装杆 <robot>.Link[1][2]
D3 mm 延长杆 <robot>.Link[1][3]
L1 mm 工具长度 <robot>.Link[2][1]
B1 mm θ2旋转中心（C2）与θ1圆（C1）中心的垂直（Z）偏移。 <robot>.Link[2][2]

通过定义z轴（z1off和z2off）的零坐标，隐含定义了两个附加参数。两个z轴在同一行应为零（见图）。 这两个将包括从轴编码器零位置到θ2的旋转轴的偏移 - 包括连接到它的所有固定的附加联轴器（在图中未示出，因为它们不交替基本机器人运动学）。

IMPORTANT.svgIMPORTANT
假设机器人具有对称的设置。 工具法兰在D2连杆的中间，theta2的旋转中心位于θ1圆的中间。 要达到这两项要求至关重要，否则运动学关系无效。

奇异点

理论上说，这些运动学有两个奇点，我们称之为滚动奇异性和连杆奇异性（这些名称只是随意地给出，因为我们需要以某种方式表示它们），但是我们将只处理一个，而另一个对用户将不可用。以下为解释:

旋转奇异点

GSR-CONFIG.PNG

当θ1和θ3都是共线的时，发生这种奇异性。 它们的和(θ1 + θ3)构建笛卡尔转角，并且这两个数字的任何组合将代表相同的转角。


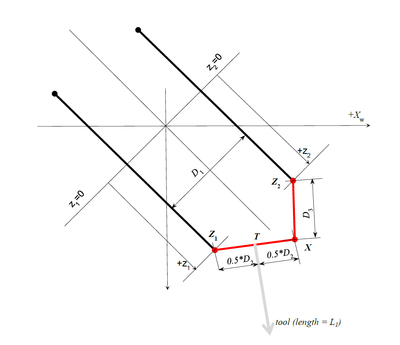
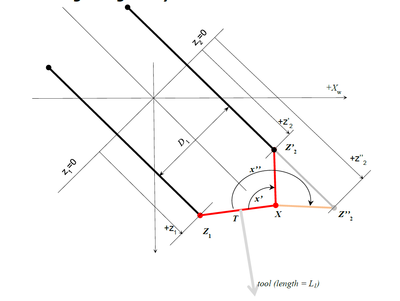
连杆奇异

GSR-RSING.PNG

这是一个典型的四杆机构奇异性，对于Z1X段的相同位置，Z2点有两个解决方案。 为了避免这种奇异点的问题，只能采取最小x角的解决方案（图中的x'角）。  

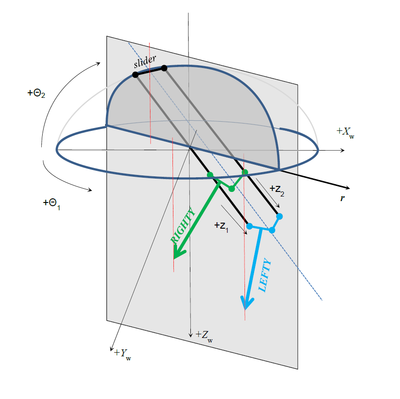
配置标志

实际上系统中应该有两个配置标志。 但是，由于其中的一个配置不允许，所以只有一个（ARM）用户可用（用于读取和写入）。

GSR-LSING.PNG

Arm配置标志根据以下定义:

如果工具尖端与θ<2>滑块位于同一侧，则为“RIGHTY”。 否则是“'LEFTY

或:

如果 r > 0，Arm 为LEFTY
如果r<0,Arm is RIGHTY

在MC-Basic语言中:


典型的机器人姿态

以下列出了一些更好地了解工作空间坐标的典型姿势。 它们不需要代表机器人的可行位置（由于某些轴位置限制），但它们是完成和测试机器人运动学定义的好例子。

GSR-POS0.PNG

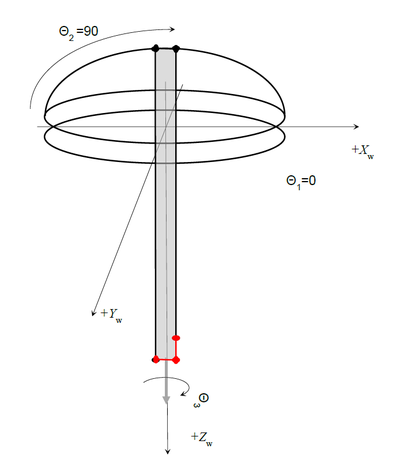
• 水平位置，俯仰角= 90度: {0,0,Z1,Z2-D3,0}  #{Z1+L1,B1,-90,0}

• 相同姿态旋转θ3 - 直接转换成旋转角度 {0,0,Z1,Z2-D3,45}  #{Z1+L1,B1,-90,45} {0,0,Z1,Z2-D3,-45}  #{Z1+L1,B1,-90,-45}


GSR-POS1.PNG


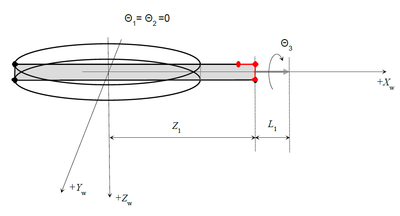
水平位置，俯仰角= ±90度: {90,0,Z1,Z1-D3,0}  #{0,-(Z1+L1),B1,-90,0} {-90,0,Z1,Z1-D3,0}  #{0,+(Z1+L1),B1,-90,0}

GSR-POS2.PNG

• 奇异点: {0,90,Z1,Z1-D3,0}  #{0,0,B1+(Z1+L1),0,0} {R,90,Z1,Z1-D3,-R}  #{0,0, B1+ (Z1+L1),0,0} for any R!

GSR light v2 sezione T2 Z out

GSR-LV02T2ZOUT.PNG 

-->move {0,90,386+76,386,0}
-->?setpoint
#{-7.41629e-14 , 0 , 743 , 0 , 0}
-->


GSR light v2 sezione T2 Z in

GSR-LV02T2ZIN.PNG 

-->move {0,90,232+76,232,0}
-->?setpoint
#{-2.26485e-14 , 0 , 589 , 0 , 0}
-->

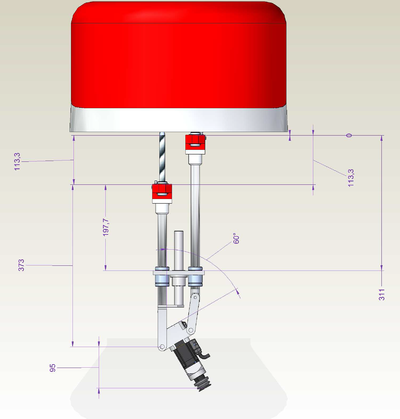
GSR light v02 Z.in T3.60

GSR-V02ZINT360.PNG 

-->moves {0,90,113.3+373,373,0}
-->?setpoint
#{60.8857 , 0 , 730.64 , -29.986 , 0}
-->?113.3+373+95+149
730.3


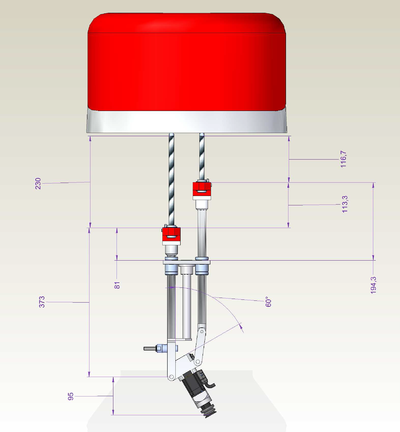
GSR light v02 Z.out T3.60

GSR-V02ZOUTT360.PNG 

-->moves {0,90,230+373,230+373-113.3,0}
-->?setpoint
#{60.8857 , 0 , 847.34 , -29.986 , 0}
-->?230+373+95+149
847
-->


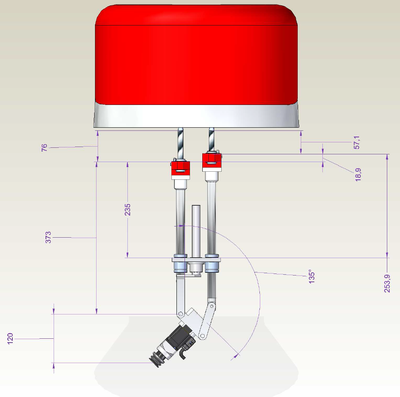
GSR light v02 Z.in T3.135

GSR-V02ZINT3135.PNG 

-->move {0,90,76+373,76+373 - 18.9,0}
-->?setpoint
#{-104.514 , 0 , 718.183 , 45.022 , 0}
-->?120+373+76+149
718
-->

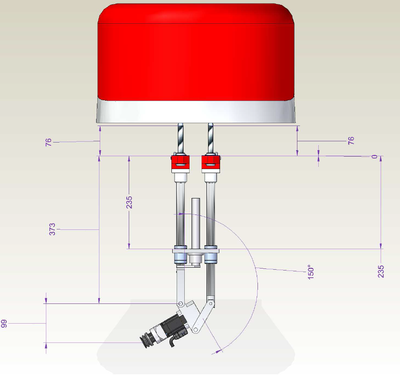
GSR light v02 Z.in T3.150

GSR-V02ZINT3150.PNG 

-->move {0,90,76+373,76+373,0}
-->?setpoint
#{-133.315 , 0 , 696.909 , 60 , 0}
-->?99+373+76+149
697

GSR light v02 Z.in T3.180

GSR-V02ZINT3180.PNG 

-->move {0,90,76+373,76+373+76,0}
-->?setpoint
#{-170 , 0 , 636 , 90 , 0}
-->?38+373+76+149
636
-->


NOTE-Info.svgNOTE
在这一点上，我们有连杆奇异点
Retrieved from "http://softmc.servotronix.com/index.php?title=Galileo_Sphere_Robot_(GSR)_Kinematics/zh-hans&oldid=129073"