AXY:Rod forces model for Delta kinematics

On a Delta robot the mechanical connection between the platform (point C) and the crank arm (Point B) is realized by a pair of parallelogram rods. The ball and socket joints at B and C can only carry a limited force, which is push/pull force of the rods. If the maximal force of the ball joints is exceeded, robot arms can hang out which leads to destruction of the robot. Because of kinematic structure of delta Robots rod forces depend on position, acceleration and moving direction. A physical model is needed to pre-compute rod forces for start/target positions and limit acceleration/deceleration according to maximal allowed forces.

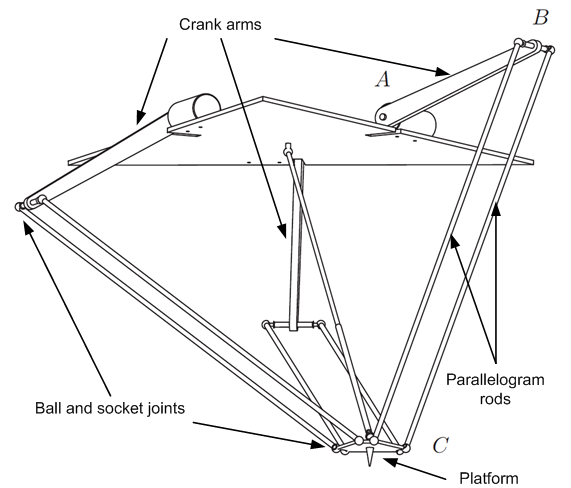
Physical model

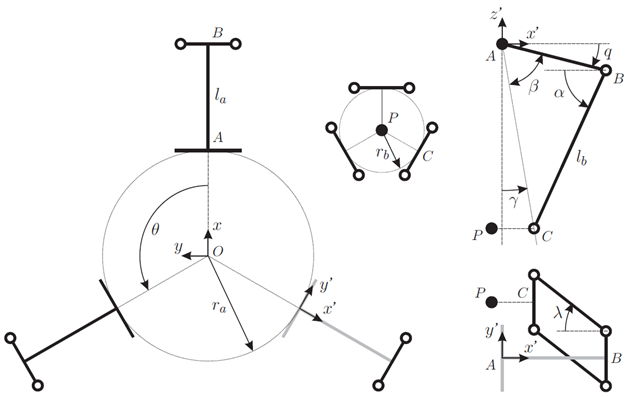
Relevant kinematic values

This rod forces model is based on the inverse dynamic model developed by IWF (File:Inverse kinematics and inverse dynamics for Delta - IWF report.pdf). The actuating joint torques $\tau _{i}$ are considered as known.

The coordinate system used by IWF differs from that used at MANZ (Y and Z directions are inverted). In this model the IWF coordinate system is used. The transformation from and into MANZ coordinate system is done by IDM implementation.

Forces at crank arms

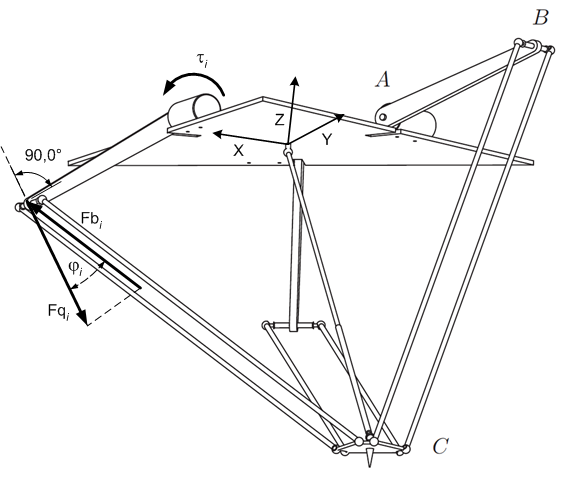
Forces at crank arms

The direction unit vector of the force ${\overrightarrow {Fq}}_{i}$ points perpendicularly to the crank arm:

${\overrightarrow {Fq}}_{i}^{*}={\begin{bmatrix}\cos \theta _{i}&-\sin \theta _{i}&0\\\sin \theta _{i}&\cos \theta _{i}&0\\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}\cos q_{i}&0&\sin q_{i}\\0&1&0\\-\sin q_{i}&0&\cos q_{i}\end{bmatrix}}\cdot {\begin{bmatrix}0\\0\\-1\end{bmatrix}}={\begin{bmatrix}-\cos \theta _{i}\cdot \sin q_{i}\\-\sin \theta _{i}\cdot \sin q_{i}\\-\cos q_{i}\end{bmatrix}}\qquad \mathrm {(1)}$

The actuating joint torques $\tau _{i}$ comprise load torque, friction torques, gravity compensation torque and dynamic torque (inertia):

$\tau _{i}=l_{a}\cdot \left|{\overrightarrow {Fq}}_{i}\right|+\rho _{v}\cdot {\dot {q}}_{i}+\rho _{c}\cdot sign({\dot {q}}_{i})-l_{AB}\cdot m_{AB}\cdot g\cdot \cos(q_{i})+\Theta _{AB}\cdot {\ddot {q}}_{i}$

The absolute value of $Fq_{i}$ is then:

$\left|{\overrightarrow {Fq}}_{i}\right|={\frac {\tau _{i}-\rho _{v}\cdot {\dot {q}}_{i}-\rho _{c}\cdot sign({\dot {q}}_{i})+l_{AB}\cdot m_{AB}\cdot g\cdot \cos(q_{i})-\Theta _{AB}\cdot {\ddot {q}}_{i}}{l_{a}}}\qquad \mathrm {(2)}$

The direction of the parallelogram rods is the connection between points C and B:

${\overrightarrow {C_{i}B_{i}}}={\begin{bmatrix}\left(r+l_{a}\cdot \cos q_{i}\right)\cdot \cos \theta _{i}-x\\\left(r+l_{a}\cdot \cos q_{i}\right)\cdot \sin \theta _{i}-y\\-l_{a}\cdot \sin q_{i}-z\end{bmatrix}}$

The direction unit vector of the force ${\overrightarrow {Fb}}_{i}$ is parallel to the parallelogram rods:

${\overrightarrow {Fb}}_{i}^{*}={\frac {\overrightarrow {C_{i}B_{i}}}{\left|{\overrightarrow {C_{i}B_{i}}}\right|}}\qquad \mathrm {(3)}$

The angle between ${\overrightarrow {Fb}}_{i}$ and ${\overrightarrow {Fq}}_{i}$ is obtained by using dot product definition:

$\cos \varphi _{i}=-{\frac {{\overrightarrow {Fq}}_{i}^{*}\cdot {\overrightarrow {Fb}}_{i}^{*}}{\left|{\overrightarrow {Fq}}_{i}^{*}\right|\cdot \left|{\overrightarrow {Fb}}_{i}^{*}\right|}}=-\left({\overrightarrow {Fq}}_{i}^{*}\cdot {\overrightarrow {Fb}}_{i}^{*}\right)$

The absolute value of ${\overrightarrow {Fb}}_{i}$ is computed as:

$\left|{\overrightarrow {Fb}}_{i}\right|={\frac {\left|{\overrightarrow {Fq}}_{i}\right|}{\cos \varphi _{i}}}\qquad \mathrm {(4)}$

Forces at the platform

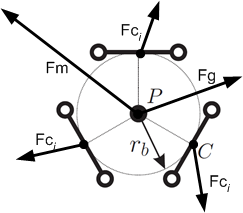
Forces at platform

The inertia of the parallelogram rods cannot be neglected. Therefore the forces at point C are less then forces at point B.

The inertia force is proportional to the Cartesian acceleration vector:

${\overrightarrow {Fm}}=-m_{platform}\cdot {\overrightarrow {\ddot {P}}}_{max}\qquad \mathrm {(5)}$

Gravity force points downward:

${\overrightarrow {Fg}}=m_{platform}\cdot g\cdot {\begin{bmatrix}0\\0\\-1\end{bmatrix}}\qquad \mathrm {(6)}$

Direction of ${\overrightarrow {Fc}}_{i}$ is identical to ${\overrightarrow {Fb}}_{i}$:

${\overrightarrow {Fc}}_{i}^{*}={\overrightarrow {Fb}}_{i}^{*}$

The unknown value of force ${\overrightarrow {Fc}}_{i}$ is expressed by a variable:

${\overrightarrow {Fc}}_{i}=\eta _{i}\cdot {\overrightarrow {Fc}}_{i}^{*}$

The sum of all forces affecting at the platform is equal zero:

${\overrightarrow {Fm}}+{\overrightarrow {Fg}}+\sum _{i}{\overrightarrow {Fc}}_{i}=0\qquad \mathrm {(7)}$

The unknown values of $\eta _{i}$ are obtained by solving the linear equation system (7).

Torques at the platform

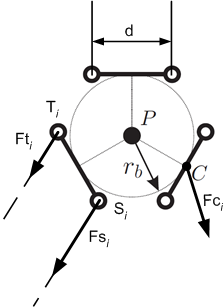
Torques at the platform

The rod forces do not affect at the platform's center of mass and therefore cause load torques which are compensated by the parallelogram structures. These compensation torques produces additional forces in the parallelogram rods and have to be modeled as well.

Load torques are obtained by considering resultant rod forces at point C:

${\overrightarrow {Ml}}_{i}={\overrightarrow {PC}}_{i}\times {\overrightarrow {Fc}}_{i}={\begin{bmatrix}r_{b}\cdot \cos \theta _{i}\\r_{b}\cdot \sin \theta _{i}\\0\end{bmatrix}}\times {\overrightarrow {Fc}}_{i}\qquad \mathrm {(8)}$

For the computation of compensation torques of both parallelogram rods are handled separately:

${\overrightarrow {Fs}}_{i}+{\overrightarrow {Ft}}_{i}={\overrightarrow {Fc}}_{i}$

The compensation torques occur because the both rod forces are different:

${\overrightarrow {Ma}}_{i}={\overrightarrow {S_{i}T_{i}}}\times \left({\overrightarrow {Fs}}_{i}-{\overrightarrow {Ft}}_{i}\right)$

The force difference of the both parallelogram rod forces is not known in first step. It is expressed by a variable $\mu _{i}$:

${\overrightarrow {Fs}}_{i}-{\overrightarrow {Ft}}_{i}=\mu _{i}\cdot {\overrightarrow {Fc}}_{i}^{*}$

For the compensation torques follows:

${\overrightarrow {Ma}}_{i}=\mu _{i}\cdot \left({\begin{bmatrix}d\cdot \sin \theta _{i}\\-d\cdot \cos \theta _{i}\\0\end{bmatrix}}\times {\overrightarrow {Fc}}_{i}^{*}\right)\qquad \mathrm {(9)}$

The addition of all load and compensation torques must be equal zero:

$\sum _{i}{\overrightarrow {Ml}}_{i}+\sum _{i}{\overrightarrow {Ma}}_{i}=0$

The unknown variables $\mu _{i}$ can be obtained by solving the linear equation system:

$\sum _{i}{\overrightarrow {Ma}}_{i}=-\sum _{i}{\overrightarrow {Ml}}_{i}\qquad \mathrm {(10)}$

Parallelogram rod forces

Because ${\overrightarrow {Fc}}_{i}^{*}$ are unity vectors, the variables $\mu _{i}$ represent the differences of the both rod forces. The absolute value of the bigger rod force is then:

$\left|{\overrightarrow {Fr}}_{i}\right|={\frac {1}{2}}\cdot \left(\left|{\overrightarrow {Fb}}_{i}\right|+\left|\mu _{i}\right|\right)\qquad \mathrm {(11)}$

Load capacity reduction due to parallelogram shift

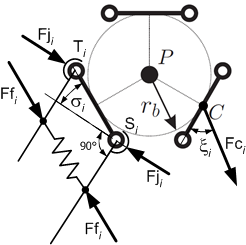
Parallelogram shift

The half-bowls of the ball and socket joints are held by a spring. For the load capacity of the joint only the force components are relevant, that are perpendicular to the rods. When the parallelogram is shifted the perpendicular forces become less and therefore the load capacity decreases.

To obtain the shift angle an intermediate step is needed:

$\cos \xi _{i}={\overrightarrow {S_{i}T_{i}}}^{*}\cdot {\overrightarrow {Fc}}_{i}^{*}={\begin{bmatrix}\sin \theta _{i}\\-\cos \theta _{i}\\0\end{bmatrix}}\cdot {\overrightarrow {Fc}}_{i}^{*}$

The reduction factor of the joint's load capacity is then:

$Rs_{i}=\cos \sigma _{i}=\sin \xi _{i}={\sqrt {1-\cos ^{2}\xi _{i}}}\qquad \mathrm {(12)}$

Limitation of acceleration/deceleration

To set appropriate acceleration and deceleration values for a given straight motion it is adequate to test only the start and target points.

The acceleration rates at start point respectively the deceleration rate at target point are computed as quotient of maximal allowed rod force and the computed rod force:

$Ra=\min _{i}{\frac {Fr_{max}\cdot Rs_{i}}{\left|{\overrightarrow {Fr}}_{i}\right|}}\qquad \mathrm {(13)}$

Parameters

The only model parameter $Fr_{max}$ can only be obtained by incrementally increasing (trial and error).

Verification

See verification page.