Dynamic Models

This page gives an overview over all implemented dynamic models.

General considerations

• Friction is handled on axis basis. The parameters for friction are set for each axis separately.
• Torque (Force) is always expressed in [Nm] ([N])
  

Rotational Axes

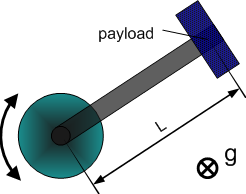
Dynamic Model 1 - simple rotary axis

Number	Parameter	Comments
1	$I$	Total moment of inertia around the rotation axis of the moved part

Model equation

$T=(I+I_{payload})\cdot acc$

Dynamic Model 2 - horizontal crank-arm axis

Horizontal crank-arm axis

Number	Parameter	Comments
1	$I$	Total moment of inertia around the rotation axis of the moved part
2	$L^{2}$	Square of length of crank arm (axis to payload)

Model equation

$T=(I+I_{payload}+L^{2}\cdot M_{payload})\cdot acc$

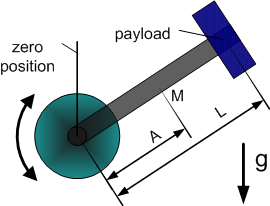
Dynamic Model 3 - vertical crank-arm axis

Vertical crank-arm axis

Number	Parameter	Comments
1	$I$	Total moment of inertia around the rotation axis of the moved part
2	$L^{2}$	Square of length of crank arm (axis to payload)
3	$M\cdot g\cdot A$	Mass (without payload) * Gravity * Distance to center of mass
4	$g\cdot L$	Gravity * Distance to Payload

Model equation

$T=(I+I_{payload}+L^{2}\cdot M_{payload})\cdot acc-(M\cdot g\cdot A+M_{payload}\cdot g\cdot L)\cdot \sin(pos)$

Linear Axes

Dynamic Model 1 - horizontal axis

Horizontal linear axis

Number	Parameter	Comments
1	$M$	Total mass of the moved part.

Model equation

$T=(M+M_{payload})\cdot acc$

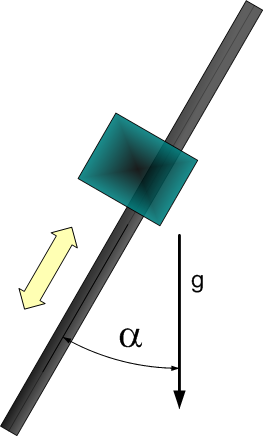
Dynamic Model 2 - vertical or tilted axis

Vertical linear axis

Number	Parameter	Comments
1	$M$	Total mass of the moved part.
2	$M\cdot g\cdot \cos(\alpha )$	Constant force due to gravity.
3	$g\cdot \cos(\alpha )$	Gravity coefficient used to consider payload mass. (g = 9.80665)

Model equation

$T=(M+M_{payload})\cdot acc+M\cdot g\cdot \cos(\alpha )+M_{payload}\cdot g\cdot \cos(\alpha )$

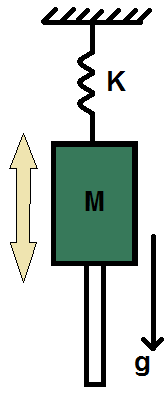
Dynamic Model 3 - vertical axis with a spring

Vertical linear axis with a spring

Number	Parameter	Comments
1	$M$	Total mass of the moved part. [kg]
2	$K$	The stiffness constant of the spring. [kg/s^2]
3	$K\cdot X_{0}$	The stiffness constant times the relaxation position of the spring. [kg*m/s^2]

Model equation

$T=(M+M_{payload})\cdot (acc+g)+K\cdot (X-X_{0})$

Traverse Arm Robots

Dynamic Model 1

Traverse Arm robot

Number	Parameter	Comments
1	$M_{1}+M_{2}$
2	$A_{2}\cdot M_{2}$
3	$A_{2}^{2}\cdot M_{2}+I_{2}$
4	$M_{3}$
5	$g\cdot M_{3}$
6	$I_{4}$
7	$J_{4}$

Scara Robots

The dynamic equations of the robot are expressed at the outputs of the gearboxes attached to the actuation motors. Therefore, the torques, joint positions, velocities, and accelerations are those of the gearbox output shafts. 

In the following models, the variables $M_{0}$ and $I_{0}$ are respectively the payload mass and payload moment of inertia relative to its center of mass. If no object or gripper is attached to the robot, the value of these variables is zero.

The variable $I_{i}$ for $i=1,...,3$ is the moment of inertia of link $i$, relative to a reference frame attached to the link's center of mass, and about the axis of rotation.

Additionally, $J_{i}$ for $i=1,...,4$ is the moment of inertia of rotor $i$, reflected to the gearbox output as follows. Let $I_{rotor,i}$ be the moment of inertia of rotor $i$ relative to a reference frame attached to the rotor's center of mass, about the rotor's axis of rotation. Let $GR_{i}$ be the gear ratio of the gearbox (including additional external gears and pulleys), then $J_{i}=I_{rotor,i}GR_{i}^{2}$.

 

Dynamic Model 1

scara robot

For non-coupled SCARA robots (axis 3 and 4 are not coupled).

Number	Parameter	Comments
1	$A_{1}^{2}M_{1}+L_{1}^{2}(M_{2}+M_{3}+M_{0})+I_{1}+J_{1}$	kg*m2
2	$A_{2}^{2}M_{2}+L_{2}^{2}(M_{3}+M_{0})+I_{2}$	kg*m2
3	$J_{2}$	kg*m2
4	$L_{1}A_{2}M_{2}+L_{1}L_{2}(M_{3}+M_{0})$	kg*m2
5	$M_{3}+M_{0}+J_{3}$	kg
6	$g(M_{3}+M_{0})$	kg*m/sec2
7	$I_{3}+I_{0}$	kg*m2
8	$J_{4}$	kg*m2

 

Dynamic Model 2

For coupled SCARA robots (axis 3 and 4 are coupled) and for concentric payloads (concentric with axis 4).

The variable $p$ is the lead of the ball screw (link 3), i.e. the linear distance traveled for each complete turn of the screw. The internal units of $p$ are [mm/deg], while its user units are [m/rad].

Number	Parameter	Comments
9	$A_{1}^{2}M_{1}+L_{1}^{2}(M_{2}+M_{3}+M_{0})+I_{1}+J_{1}$	kg*m2
10	$A_{2}^{2}M_{2}+L_{2}^{2}(M_{3}+M_{0})+I_{2}$	kg*m2
11	$L_{1}A_{2}M_{2}+L_{1}L_{2}(M_{3}+M_{0})$	kg*m2
12	$M_{3}+M_{0}$	kg
13	$I_{3}+I_{0}$	kg*m2
14	$J_{2}$	kg*m2
15	$J_{3}$	kg
16	$(M_{3}+M_{0})p^{2}+J_{4}$	kg*m2

 

The payload parameters for Dynamic Model 1 and Dynamic Model 2 are:

Number	Parameter	Comments
1	payloadMass	$M_{0}$, the mass of the payload
2	payloadInertia	$I_{0}$, the Inertia of the payload relative to its center of mass

Dynamic Model 3

For coupled SCARA robots (axis 3 and 4 are coupled) and for non-concentric payloads (non-concentric with axis 4).
The dynamic parameters are the same as model 2.

The payload parameters are:

Number	Parameter	Comments
1	payloadMass	The mass of the payload
2	payloadInertia	The Inertia of the payload relative to its center of mass
4	payloadLx	The distance to the center of mass from the 4th axis in the x direction

When using identification with this model, all of the payload parameters can be found.

 

Dynamic Model 4

Same as Dynamic Model 3.
This model is used in identification process in order to identify the payloadMass parameter only, by moving only joint number 3.

 

Dynamic Model 5

Same as Dynamic Model 3.
This model is used in identification process in order to identify the payloadInertia and payloadLx parameters, by moving only joint number 4 and very small movements in joints 1 and 2.

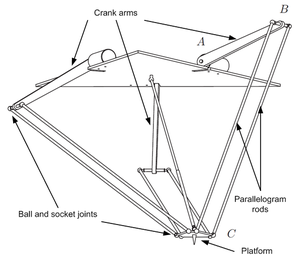
Delta Robots

Dynamic Model 1

Delta robot

Number	Parameter	Comments
1	$\Theta _{AB}$	kg*m2
2	$g\cdot L_{AB}\cdot M_{AB}$	kg*m2/sec2
3	$M_{BC}$	kg
4	$\Theta _{BC}$	kg*m2
5	$M_{P}$	kg
6	$M_{T}$	kg
7	$\Theta _{T}$	kg*m2
8	$\Theta _{T\phi }$	kg*m2
9	$L_{TO}$	m
10	$L_{TP}$	m
11	$D$
12	$C_{r}$
13	$Fr_{max}$
14	$R_{ext}$

Puma Robots

Dynamic Model 1

Puma robot

Description:

• $g$ - Gravity constant
• $m_{i}$ - Mass of the i^th link
• $a_{i}$ - length of the common normal between the i^th and i^th+1 joints
• $d_{i}$ - offset along z axis between the i^th and i^th+1 joints
• $l_{i}$ - The distance from the i^th joint to the center of mass of the i^th link

Number	Parameter	Comments
1	$I_{1}=I_{1,zz}+m_{1}*l_{1,y}^{2}+m_{2}*d_{2}^{2}+(m_{4}+m_{5}+m_{6})*a_{3}^{2}+m_{2}*l_{2,z}^{2}+$ $(m_{3}+m_{4}+m_{5}+m_{6})*(d_{2}+d_{3})^{2}+I_{2,xx}+I_{3,yy}+2*m_{2}*d_{2}*l_{2,z}+m_{2}*l_{2,y}^{2}+m_{3}*l_{3,z}^{2}+2*m_{3}*(d_{2}+d_{3})*l_{3,z}+I_{4,zz}+I_{4,yy}+I_{6,zz}$	kg*m^2
2	$I_{2}=I_{2,zz}+m_{2}*(l_{2,x}^{2}+l_{2,y}^{2})+(m_{3}+m_{4}+m_{5}+m_{6}*a_{2}^{2}$	kg*m^2
3	$I_{3}=-I_{2,xx}+I_{2,yy}+(m_{3}+m_{4}+m_{5}+m_{6})*a_{2}^{2}+m_{2}*l_{2,x}^{2}-m_{2}*l_{2,y}^{2}$	kg*m^2
4	$I_{4}=m_{2}*l_{2,x}*(d_{2}+l_{2,z})+m_{3}*a_{2}*l_{3,z}+(m_{3}+m_{4}+m_{5}+m_{6})*a_{2}*(d_{2}+d_{3})$	kg*m^2
5	$I_{5}=-m_{3}*a_{2}*l_{3,y}+(m_{4}+m_{5}+m_{6})*a_{2}*d_{4}+m_{4}*a_{2}*l_{4,z}$	kg*m^2
6	$I_{6}=I_{3,zz}+m_{3}*l_{3,y}^{2}+m_{4}*a_{3}^{2}+m_{4}*(d_{4}+l_{4,z})^{2}+I_{4,yy}+m_{5}*a_{3}^{2}+m_{5}*d_{4}^{2}+I_{5,zz}+m_{6}*a_{3}^{2}+m_{6}*d_{4}^{2}+m_{6}*l_{6,z}^{2}+I_{6,xx}$	kg*m^2
7	$I_{7}=m_{3}*l_{3,y}^{2}+I_{3,xx}-I_{3,yy}+m_{4}*l_{4,z}^{2}+2*m_{4}*d_{4}*l_{4,z}+(m_{4}+m_{5}+m_{6})*(d_{4}^{2}-a_{3}^{2})+I_{4,yy}-I_{4,yy}+I_{5,zz}-I_{5,yy}+m_{6}*l_{6,z}^{2}-I_{6,zz}+I_{6,xx}$	kg*m^2
8	$I_{8}=-m_{4}*(d_{2}+d_{3})*(d_{4}+l_{4,z})-(m_{3}+m_{6})*(d_{2}+d_{3})*d_{4}+m_{3}*l_{3,y}*l_{3,z}+m_{3}*(d_{2}+d_{3})*l_{3,y}$	kg*m^2
9	$I_{9}=m_{2}*l_{2,y}*(d_{2}+l_{2,z})$	kg*m^2
10	$I_{10}=2*m_{4}*a_{5}*l_{4,z}+2*(m_{4}+m_{5}+m_{6})*a_{3}*d_{4}$	kg*m^2
11	$I_{11}=-2*m_{2}*l_{2,x}*l_{2,y}$	kg*m^2
12	$I_{12}=(m_{4}+m_{5}+m_{6})*a_{2}*a_{3}$	kg*m^2
13	$I_{13}=(m_{4}+m_{5}+m_{6})*a_{3}*(d_{2}+d_{3})$	kg*m^2
14	$I_{14}=I_{4,zz}+I_{5,yy}+I_{6,zz}$	kg*m^2
15	$I_{15}=m_{6}*d_{4}*l_{6,z}$	kg*m^2
16	$I_{16}=m_{6}*a_{2}*l_{6,z}$	kg*m^2
17	$I_{17}=I_{5,zz}+I_{6,xx}+m_{6}*l_{6,z}^{2}$	kg*m^2
18	$I_{18}=m_{6}*(d_{2}+d_{3})*l_{6,z}$	kg*m^2
19	$I_{19}=I_{4,yy}-I_{4,xx}+I_{5,zz}-i_{5,yy}+m_{6}*l_{6,z}^{2}+I_{6,xx}-I_{6,zz}$	kg*m^2
20	$I_{20}=I_{5,yy}-I_{5,xx}-m_{6}*l_{6,z}^{2}+I_{6,zz}-I_{6,xx}$	kg*m^2
21	$I_{21}=I_{4,xx}-I_{4,yy}+I_{5,xx}-I_{5,zz}$	kg*m^2
22	$I_{22}=m_{6}*a_{3}*l_{6,z}$	kg*m^2
23	$I_{23}=I_{6,zz}$	kg*m^2

Dynamic Model 2 - Gravity

This dynamic model is for cases where the robot moves very slowly.
In such cases, the accelerations and velocities of the joints of the robot have little effect on the joints torques. The joints torques are mainly affected by gravity and friction.
This model includes only the gravity and friction part of the PUMA robot dynamic model.

Number	Parameter	Comments
1	$g(m_{2}l_{2}+a_{2}(m_{3}+m_{4}+m_{5}+m_{6}))$	kg*m^2/s^2
2	$g(m_{3}l_{3,y}+a_{3}(m_{4}+m_{5}+m_{6}))$	kg*m^2/s^2
3	$g(m_{3}l_{3,y}+m_{4}(l_{4}+d_{4}(m_{5}+m_{6}))$	kg*m^2/s^2
4	$gl_{56}(m_{5}+m_{6})$	kg*m^2/s^2

Galileo Spherical Robots (GSR)

Dynamic Model 1

Galileo robot

Number	Parameter	Comments
1	mP	Payload mass [kg]
2	mB	Balance mass [kg]
3	TP	Payload mass center distance from the flange [mm]
4	TB	Balance mass center distance from the (0,0) [mm]
5	IR	Inertia of the payload around roll [kg*m2