Difference between revisions of "Dynamic Models"
(→Dynamic Model 1: change kg/m^2 to kg*m^2) |
(→Linear Axes: add vertical liner axis with a spring) |
||
| Line 105: | Line 105: | ||
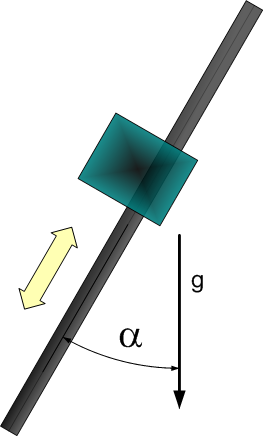
: <math>T = (M + M_{payload}) \cdot acc + M \cdot g \cdot \cos(\alpha) + M_{payload} \cdot g \cdot \cos(\alpha)</math> | : <math>T = (M + M_{payload}) \cdot acc + M \cdot g \cdot \cos(\alpha) + M_{payload} \cdot g \cdot \cos(\alpha)</math> | ||
| + | <br style="clear: both" /> | ||
| + | === Dynamic Model 3 - vertical axis with a spring === | ||
| + | {|border="1" width="80%" | ||
| + | !width="100"|Number | ||
| + | !width="250"|Parameter | ||
| + | !Comments | ||
| + | |- | ||
| + | |1 | ||
| + | |<math>M</math> | ||
| + | |Total mass of the moved part. [kg] | ||
| + | |- | ||
| + | |2 | ||
| + | |<math>K</math> | ||
| + | |The stiffness constant of the spring. [kg/s^2] | ||
| + | |- | ||
| + | |3 | ||
| + | |<math>K \cdot X_{0}</math> | ||
| + | |The stiffness constant times the relaxation position of the spring. [kg*m/s^2] | ||
| + | |} | ||
| + | ;Model equation | ||
| + | : <math>T = (M + M_{payload}) \cdot (acc + g) + K\cdot (X-X_{0})</math> | ||
== Traverse Arm Robots == | == Traverse Arm Robots == | ||
Revision as of 07:43, 4 September 2018
This page gives an overview over all implemented dynamic models.
General considerations
- Friction is handled on axis basis. The parameters for friction are set for each axis separately.
- Torque (Force) is always expressed in [Nm] ([N])
Contents
Rotational Axes
Dynamic Model 1 - simple rotary axis
| Number | Parameter | Comments |
|---|---|---|
| 1 | Total moment of inertia around the rotation axis of the moved part |
- Model equation
Dynamic Model 2 - horizontal crank-arm axis
| Number | Parameter | Comments |
|---|---|---|
| 1 | Total moment of inertia around the rotation axis of the moved part | |
| 2 | Square of length of crank arm (axis to payload) |
- Model equation
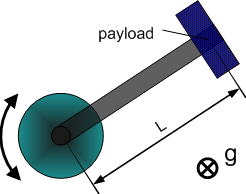
Dynamic Model 3 - vertical crank-arm axis
| Number | Parameter | Comments |
|---|---|---|
| 1 | Total moment of inertia around the rotation axis of the moved part | |
| 2 | Square of length of crank arm (axis to payload) | |
| 3 | Mass (without payload) * Gravity * Distance to center of mass | |
| 4 | Gravity * Distance to Payload |
- Model equation
Linear Axes
Dynamic Model 1 - horizontal axis
| Number | Parameter | Comments |
|---|---|---|
| 1 | Total mass of the moved part. |
- Model equation
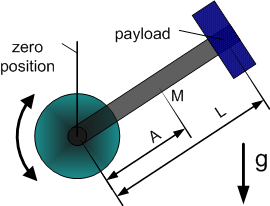
Dynamic Model 2 - vertical or tilted axis
| Number | Parameter | Comments |
|---|---|---|
| 1 | Total mass of the moved part. | |
| 2 | Constant force due to gravity. | |
| 3 | Gravity coefficient used to consider payload mass. (g = 9.80665) |
- Model equation
Dynamic Model 3 - vertical axis with a spring
| Number | Parameter | Comments |
|---|---|---|
| 1 | Total mass of the moved part. [kg] | |
| 2 | The stiffness constant of the spring. [kg/s^2] | |
| 3 | The stiffness constant times the relaxation position of the spring. [kg*m/s^2] |
- Model equation
Traverse Arm Robots
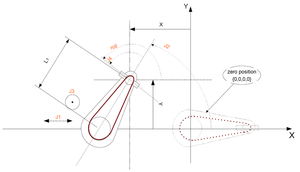
Dynamic Model 1
| Number | Parameter | Comments |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 |
Scara Robots
Dynamic Model 1
| Number | Parameter | Comments |
|---|---|---|
| 1 | ||
| 2 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A_2^2 \cdot M_2 + I_2} | |
| 3 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle J_2} | |
| 4 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L_1 \cdot A_2 \cdot M_2} | |
| 5 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M_3} | |
| 6 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g \cdot M_3} | |
| 7 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_4} | |
| 8 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle J_4} |
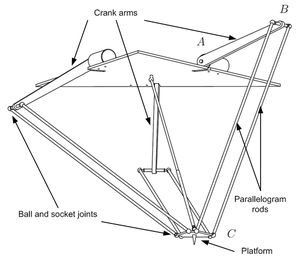
Delta Robots
Dynamic Model 1
| Number | Parameter | Comments |
|---|---|---|
| 1 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Theta_{AB}} | kg*m2 |
| 2 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g \cdot L_{AB} \cdot M_{AB}} | kg*m2/sec2 |
| 3 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M_{BC}} | kg |
| 4 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Theta_{BC}} | kg*m2 |
| 5 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M_P} | kg |
| 6 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M_T} | kg |
| 7 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Theta_T} | kg*m2 |
| 8 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Theta_{T\phi}} | kg*m2 |
| 9 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L_{TO}} | m |
| 10 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L_{TP}} | m |
| 11 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle D} | |
| 12 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle C_r} | |
| 13 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Fr_{max}} | |
| 14 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R_{ext}} |
Puma Robots
Dynamic Model 1
Description:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g } - Gravity constant
- - Mass of the ith link
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_{i} } - length of the common normal between the ith and ith+1 joints
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d_{i} } - offset along z axis between the ith and ith+1 joints
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle l_{i} } - The distance from the ith joint to the center of mass of the ith link
| Number | Parameter | Comments |
|---|---|---|
| 1 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{1} = I_{1,zz}+m_{1}*l_{1,y}^2 +m_{2}*d_{2}^2+(m_{4}+m_{5}+m_{6})*a_{3}^2+m_{2}*l_{2,z}^2+}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (m_{3}+m_{4}+m_{5}+m_{6})*(d_{2}+d_{3})^2+I_{2,xx}+I_{3,yy}+2*m_{2}*d_{2}*l_{2,z}+m_{2}*l_{2,y}^2+m_{3}*l_{3,z}^2+2*m_{3}*(d_{2}+d_{3})*l_{3,z}+I_{4,zz}+I_{4,yy}+I_{6,zz}} |
kg*m^2 |
| 2 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{2} = I_{2,zz}+m_{2}*(l_{2,x}^2+l_{2,y}^2)+(m_{3}+m_{4}+m_{5}+m_{6}*a_{2}^2} | kg*m^2 |
| 3 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{3} = -I_{2,xx}+I_{2,yy}+(m_{3}+m_{4}+m_{5}+m_{6})*a_{2}^2+m_{2}*l_{2,x}^2-m_{2}*l_{2,y}^2} | kg*m^2 |
| 4 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{4} = m_{2}*l_{2,x}*(d_{2}+l_{2,z})+m_{3}*a_{2}*l_{3,z}+(m_{3}+m_{4}+m_{5}+m_{6})*a_{2}*(d_{2}+d_{3})} | kg*m^2 |
| 5 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{5} = -m_{3}*a_{2}*l_{3,y}+(m_{4}+m_{5}+m_{6})*a_{2}*d_{4}+m_{4}*a_{2}*l_{4,z}} | kg*m^2 |
| 6 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{6} = I_{3,zz}+m_{3}*l_{3,y}^2+m_{4}*a_{3}^2+m_{4}*(d_{4}+l_{4,z})^2+I_{4,yy}+m_{5}*a_{3}^2+m_{5}*d_{4}^2+I_{5,zz}+m_{6}*a_{3}^2+m_{6}*d_{4}^2+m_{6}*l_{6,z}^2+I_{6,xx}} | kg*m^2 |
| 7 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{7} = m_{3}*l_{3,y}^2+I_{3,xx}-I_{3,yy}+m_{4}*l_{4,z}^2+2*m_{4}*d_{4}*l_{4,z}+(m_{4}+m_{5}+m_{6})*(d_{4}^2-a_{3}^2)+I_{4,yy}-I_{4,yy}+I_{5,zz}-I_{5,yy}+m_{6}*l_{6,z}^2-I_{6,zz}+I_{6,xx}} | kg*m^2 |
| 8 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{8} = -m_{4}*(d_{2}+d_{3})*(d_{4}+l_{4,z})-(m_{3}+m_{6})*(d_{2}+d_{3})*d_{4}+m_{3}*l_{3,y}*l_{3,z}+m_{3}*(d_{2}+d_{3})*l_{3,y}} | kg*m^2 |
| 9 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{9} = m_{2}*l_{2,y}*(d_{2}+l_{2,z})} | kg*m^2 |
| 10 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{10} = 2*m_{4}*a_{5}*l_{4,z}+2*(m_{4}+m_{5}+m_{6})*a_{3}*d_{4}} | kg*m^2 |
| 11 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{11} = -2*m_{2}*l_{2,x}*l_{2,y}} | kg*m^2 |
| 12 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{12} = (m_{4}+m_{5}+m_{6})*a_{2}*a_{3}} | kg*m^2 |
| 13 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{13} = (m_{4}+m_{5}+m_{6})*a_{3}*(d_{2}+d_{3})} | kg*m^2 |
| 14 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{14} = I_{4,zz}+I_{5,yy}+I_{6,zz}} | kg*m^2 |
| 15 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{15} = m_{6}*d_{4}*l_{6,z}} | kg*m^2 |
| 16 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{16} = m_{6}*a_{2}*l_{6,z}} | kg*m^2 |
| 17 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{17} = I_{5,zz}+I_{6,xx}+m_{6}*l_{6,z}^2} | kg*m^2 |
| 18 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{18} = m_{6}*(d_{2}+d_{3})*l_{6,z}} | kg*m^2 |
| 19 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{19} = I_{4,yy}-I_{4,xx}+I_{5,zz}-i_{5,yy}+m_{6}*l_{6,z}^2+I_{6,xx}-I_{6,zz}} | kg*m^2 |
| 20 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{20} = I_{5,yy}-I_{5,xx}-m_{6}*l_{6,z}^2+I_{6,zz}-I_{6,xx}} | kg*m^2 |
| 21 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{21} = I_{4,xx}-I_{4,yy}+I_{5,xx}-I_{5,zz}} | kg*m^2 |
| 22 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{22} = m_{6}*a_{3}*l_{6,z}} | kg*m^2 |
| 23 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I_{23} = I_{6,zz}} | kg*m^2 |
Dynamic Model 2 - Gravity
| Number | Parameter | Comments |
|---|---|---|
| 1 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g(m_{2}l_{2}+a_{2}(m_{3}+m_{4}+m_{5}+m_{6}))} | kg*m^2/s^2 |
| 2 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g(m_{3}l_{3,y}+a_{3}(m_{4}+m_{5}+m_{6}))} | kg*m^2/s^2 |
| 3 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g(m_{3}l_{3,y}+m_{4}(l_{4}+d_{4}(m_{5}+m_{6}))} | kg*m^2/s^2 |
| 4 | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle gl_{56}(m_{5}+m_{6})} | kg*m^2/s^2 |
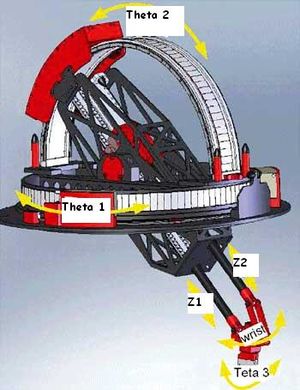
Galileo Spherical Robots (GSR)
Dynamic Model 1
| Number | Parameter | Comments |
|---|---|---|
| 1 | mP | Payload mass [kg] |
| 2 | mB | Balance mass [kg] |
| 3 | TP | Payload mass center distance from the flange [mm] |
| 4 | TB | Balance mass center distance from the (0,0) [mm] |
| 5 | IR | Inertia of the payload around roll [kg*m2 |