Dynamic Models

This page gives an overview over all implemented dynamic models.

General considerations

• Friction is handled on axis basis. The parameters for friction are set for each axis separately.
• Torque (Force) is always expressed in [Nm] ([N])
  

Rotational Axes

Dynamic Model 1 - simple rotary axis

Number	Parameter	Comments
1	$I$	Total moment of inertia around the rotation axis of the moved part

Model equation

$T=(I+I_{payload})\cdot acc$

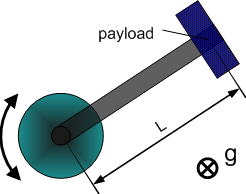
Dynamic Model 2 - horizontal crank-arm axis

Horizontal crank-arm axis

Number	Parameter	Comments
1	$I$	Total moment of inertia around the rotation axis of the moved part
2	$L^{2}$	Square of length of crank arm (axis to payload)

Model equation

$T=(I+I_{payload}+L^{2}\cdot M_{payload})\cdot acc$

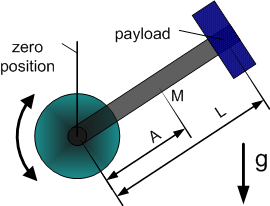
Dynamic Model 3 - vertical crank-arm axis

Vertical crank-arm axis

Number	Parameter	Comments
1	$I$	Total moment of inertia around the rotation axis of the moved part
2	$L^{2}$	Square of length of crank arm (axis to payload)
3	$M\cdot g\cdot A$	Mass (without payload) * Gravity * Distance to center of mass
4	$g\cdot L$	Gravity * Distance to Payload

Model equation

$T=(I+I_{payload}+L^{2}\cdot M_{payload})\cdot acc-(M\cdot g\cdot A+M_{payload}\cdot g\cdot L)\cdot \sin(pos)$

Linear Axes

Dynamic Model 1 - horizontal axis

Horizontal linear axis

Number	Parameter	Comments
1	$M$	Total mass of the moved part.

Model equation

$T=(M+M_{payload})\cdot acc$

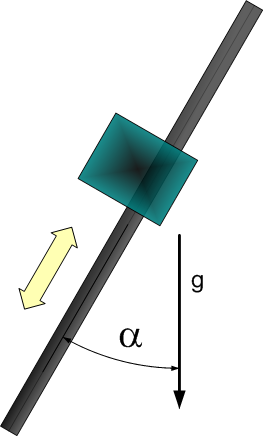
Dynamic Model 2 - vertical or tilted axis

Vertical linear axis

Number	Parameter	Comments
1	$M$	Total mass of the moved part.
2	$M\cdot g\cdot \cos(\alpha )$	Constant force due to gravity.
3	$g\cdot \cos(\alpha )$	Gravity coefficient used to consider payload mass. (g = 9.80665)

Model equation

$T=(M+M_{payload})\cdot acc+M\cdot g\cdot \cos(\alpha )+M_{payload}\cdot g\cdot \cos(\alpha )$

Traverse Arm Robots

Dynamic Model 1

Traverse Arm robot

Number	Parameter	Comments
1	$M_{1}+M_{2}$
2	$A_{2}\cdot M_{2}$
3	$A_{2}^{2}\cdot M_{2}+I_{2}$
4	$M_{3}$
5	$g\cdot M_{3}$
6	$I_{4}$
7	$J_{4}$

Scara Robots

Dynamic Model 1

scara robot

Number	Parameter	Comments
1	$L_{1}^{2}\cdot M_{2}+I_{1}$
2	$A_{2}^{2}\cdot M_{2}+I_{2}$
3	$J_{2}$
4	$L_{1}\cdot A_{2}\cdot M_{2}$
5	$M_{3}$
6	$g\cdot M_{3}$
7	$I_{4}$
8	$J_{4}$

Delta Robots

Dynamic Model 1

Delta robot

Number	Parameter	Comments
1	$\Theta _{AB}$	kg*m2
2	$g\cdot L_{AB}\cdot M_{AB}$	kg*m2/sec2
3	$M_{BC}$	kg
4	$\Theta _{BC}$	kg*m2
5	$M_{P}$	kg
6	$M_{T}$	kg
7	$\Theta _{T}$	kg*m2
8	$\Theta _{T\phi }$	kg*m2
9	$L_{TO}$	m
10	$L_{TP}$	m
11	$D$
12	$C_{r}$
13	$Fr_{max}$
14	$R_{ext}$

Puma Robots

Dynamic Model 1

Puma robot

Description:

• $g$ - The gravity constant
• $m_{i}$ - The mass of the i^th link
• $a_{i}$ - The length of the i^th link
• $l_{i}$ - The distance from the i^th joint to the center of mass of the i^th link

Number	Parameter	Comments
1	$I_{1}=I_{1,zz}+m_{1}*l_{1,y}^{2}+m_{2}*d_{2}^{2}+(m_{4}+m_{5}+m_{6})*a_{3}^{2}+m_{2}*l_{2,z}^{2}+$ $(m_{3}+m_{4}+m_{5}+m_{6})*(d_{2}+d_{3})^{2}+I_{2,xx}+I_{3,yy}+2*m_{2}*d_{2}*l_{2,z}+m_{2}*l_{2,y}^{2}+m_{3}*l_{3,z}^{2}+2*m_{3}*(d_{2}+d_{3})*l_{3,z}+I_{4,zz}+I_{4,yy}+I_{6,zz}$	kg/m^2
2	$g(m_{3}l_{3,y}+l_{3}(m_{4}+m_{5}+m_{6}))$	kg*m^2/s^2
3	$g(m_{3}l_{3,y}+l_{3}(m_{4}+m_{5}+m_{6}))$	kg*m^2/s^2
4	$gl_{56}(m_{5}+m_{6})$	kg*m^2/s^2

Dynamic Model 2 - Gravity

Puma robot

Description:

• $g$ - The gravity constant
• $m_{i}$ - The mass of the i^th link
• $a_{i}$ - The length of the i^th link
• $l_{i}$ - The distance from the i^th joint to the center of mass of the i^th link

Number	Parameter	Comments
1	$g(m_{2}l_{2}+a_{2}(m_{3}+m_{4}+m_{5}+m_{6}))$	kg*m^2/s^2
2	$g(m_{3}l_{3,y}+l_{3}(m_{4}+m_{5}+m_{6}))$	kg*m^2/s^2
3	$g(m_{3}l_{3,y}+l_{3}(m_{4}+m_{5}+m_{6}))$	kg*m^2/s^2
4	$gl_{56}(m_{5}+m_{6})$	kg*m^2/s^2

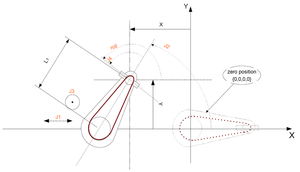
Galileo Spherical Robots (GSR)

Dynamic Model 1

Galileo robot

Number	Parameter	Comments
1	mP	Payload mass [kg]
2	mB	Balance mass [kg]
3	TP	Payload mass center distance from the flange [mm]
4	TB	Balance mass center distance from the (0,0) [mm]
5	IR	Inertia of the payload around roll [kg*m2