Dynamic Models

This page gives an overview over all implemented dynamic models.

General considerations

• Friction is handled on axis basis. The parameters for friction are set for each axis separately.
• Torque (Force) is always expressed in [Nm] ([N])
  

Rotational Axes

Dynamic Model 1 - simple rotary axis

Number	Parameter	Comments
1	$I$	Total moment of inertia around the rotation axis of the moved part

Model equation

$T=(I+I_{payload})\cdot acc$

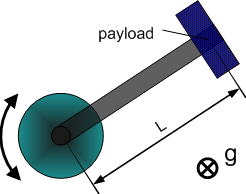
Dynamic Model 2 - horizontal crank-arm axis

Horizontal crank-arm axis

Number	Parameter	Comments
1	$I$	Total moment of inertia around the rotation axis of the moved part
2	$L^{2}$	Square of length of crank arm (axis to payload)

Model equation

$T=(I+I_{payload}+L^{2}\cdot M_{payload})\cdot acc$

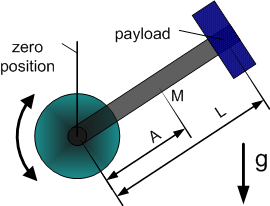
Dynamic Model 3 - vertical crank-arm axis

Vertical crank-arm axis

Number	Parameter	Comments
1	$I$	Total moment of inertia around the rotation axis of the moved part
2	$L^{2}$	Square of length of crank arm (axis to payload)
3	$M\cdot g\cdot A$	Mass (without payload) * Gravity * Distance to center of mass
4	$g\cdot L$	Gravity * Distance to Payload

Model equation

$T=(I+I_{payload}+L^{2}\cdot M_{payload})\cdot acc-(M\cdot g\cdot A+M_{payload}\cdot g\cdot L)\cdot \sin(pos)$

Linear Axes

Dynamic Model 1 - horizontal axis

Horizontal linear axis

Number	Parameter	Comments
1	$M$	Total mass of the moved part.

Model equation

$T=(M+M_{payload})\cdot acc$

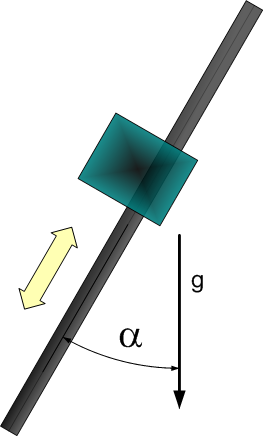
Dynamic Model 2 - vertical or tilted axis

Vertical linear axis

Number	Parameter	Comments
1	$M$	Total mass of the moved part.
2	$M\cdot g\cdot \cos(\alpha )$	Constant force due to gravity.
3	$g\cdot \cos(\alpha )$	Gravity coefficient used to consider payload mass. (g = 9.80665)

Model equation

$T=(M+M_{payload})\cdot acc+M\cdot g\cdot \cos(\alpha )+M_{payload}\cdot g\cdot \cos(\alpha )$

Traverse Arm Robots

Dynamic Model 1

Traverse Arm robot

Number	Parameter	Comments
1	$M_{1}+M_{2}$
2	$A_{2}\cdot M_{2}$
3	$A_{2}^{2}\cdot M_{2}+I_{2}$
4	$M_{3}$
5	$g\cdot M_{3}$
6	$I_{4}$
7	$J_{4}$

Scara Robots

Dynamic Model 1

scara robot

Number	Parameter	Comments
1	$L_{1}^{2}\cdot M_{2}+I_{1}$
2	$A_{2}^{2}\cdot M_{2}+I_{2}$
3	$J_{2}$
4	$L_{1}\cdot A_{2}\cdot M_{2}$
5	$M_{3}$
6	$g\cdot M_{3}$
7	$I_{4}$
8	$J_{4}$

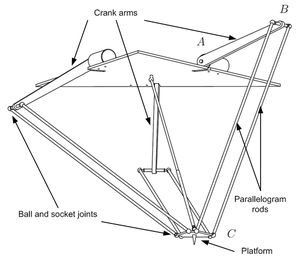
Delta Robots

Dynamic Model 1

Delta robot

Number	Parameter	Comments
1	$\Theta _{AB}$	kg*m2
2	$g\cdot L_{AB}\cdot M_{AB}$	kg*m2/sec2
3	$M_{BC}$	kg
4	$\Theta _{BC}$	kg*m2
5	$M_{P}$	kg
6	$M_{T}$	kg
7	$\Theta _{T}$	kg*m2
8	$\Theta _{T\phi }$	kg*m2
9	$L_{TO}$	m
10	$L_{TP}$	m
11	$D$
12	$C_{r}$
13	$Fr_{max}$
14	$R_{ext}$

Puma Robots

Dynamic Model 1

Puma robot

Description:

• $g$ - Gravity constant
• $m_{i}$ - Mass of the i^th link
• $a_{i}$ - length of the common normal between the i^th and i^th+1 joints
• $d_{i}$ - offset along z axis between the i^th and i^th+1 joints
• $l_{i}$ - The distance from the i^th joint to the center of mass of the i^th link

Number	Parameter	Comments
1	$I_{1}=I_{1,zz}+m_{1}*l_{1,y}^{2}+m_{2}*d_{2}^{2}+(m_{4}+m_{5}+m_{6})*a_{3}^{2}+m_{2}*l_{2,z}^{2}+$ $(m_{3}+m_{4}+m_{5}+m_{6})*(d_{2}+d_{3})^{2}+I_{2,xx}+I_{3,yy}+2*m_{2}*d_{2}*l_{2,z}+m_{2}*l_{2,y}^{2}+m_{3}*l_{3,z}^{2}+2*m_{3}*(d_{2}+d_{3})*l_{3,z}+I_{4,zz}+I_{4,yy}+I_{6,zz}$	kg*m^2
2	$I_{2}=I_{2,zz}+m_{2}*(l_{2,x}^{2}+l_{2,y}^{2})+(m_{3}+m_{4}+m_{5}+m_{6}*a_{2}^{2}$	kg*m^2
3	$I_{3}=-I_{2,xx}+I_{2,yy}+(m_{3}+m_{4}+m_{5}+m_{6})*a_{2}^{2}+m_{2}*l_{2,x}^{2}-m_{2}*l_{2,y}^{2}$	kg*m^2
4	$I_{4}=m_{2}*l_{2,x}*(d_{2}+l_{2,z})+m_{3}*a_{2}*l_{3,z}+(m_{3}+m_{4}+m_{5}+m_{6})*a_{2}*(d_{2}+d_{3})$	kg*m^2
5	$I_{5}=-m_{3}*a_{2}*l_{3,y}+(m_{4}+m_{5}+m_{6})*a_{2}*d_{4}+m_{4}*a_{2}*l_{4,z}$	kg*m^2
6	$I_{6}=I_{3,zz}+m_{3}*l_{3,y}^{2}+m_{4}*a_{3}^{2}+m_{4}*(d_{4}+l_{4,z})^{2}+I_{4,yy}+m_{5}*a_{3}^{2}+m_{5}*d_{4}^{2}+I_{5,zz}+m_{6}*a_{3}^{2}+m_{6}*d_{4}^{2}+m_{6}*l_{6,z}^{2}+I_{6,xx}$	kg*m^2
7	$I_{7}=m_{3}*l_{3,y}^{2}+I_{3,xx}-I_{3,yy}+m_{4}*l_{4,z}^{2}+2*m_{4}*d_{4}*l_{4,z}+(m_{4}+m_{5}+m_{6})*(d_{4}^{2}-a_{3}^{2})+I_{4,yy}-I_{4,yy}+I_{5,zz}-I_{5,yy}+m_{6}*l_{6,z}^{2}-I_{6,zz}+I_{6,xx}$	kg*m^2
8	$I_{8}=-m_{4}*(d_{2}+d_{3})*(d_{4}+l_{4,z})-(m_{3}+m_{6})*(d_{2}+d_{3})*d_{4}+m_{3}*l_{3,y}*l_{3,z}+m_{3}*(d_{2}+d_{3})*l_{3,y}$	kg*m^2
9	$I_{9}=m_{2}*l_{2,y}*(d_{2}+l_{2,z})$	kg*m^2
10	$I_{10}=2*m_{4}*a_{5}*l_{4,z}+2*(m_{4}+m_{5}+m_{6})*a_{3}*d_{4}$	kg*m^2
11	$I_{11}=-2*m_{2}*l_{2,x}*l_{2,y}$	kg*m^2
12	$I_{12}=(m_{4}+m_{5}+m_{6})*a_{2}*a_{3}$	kg*m^2
13	$I_{13}=(m_{4}+m_{5}+m_{6})*a_{3}*(d_{2}+d_{3})$	kg*m^2
14	$I_{14}=I_{4,zz}+I_{5,yy}+I_{6,zz}$	kg*m^2
15	$I_{15}=m_{6}*d_{4}*l_{6,z}$	kg*m^2
16	$I_{16}=m_{6}*a_{2}*l_{6,z}$	kg*m^2
17	$I_{17}=I_{5,zz}+I_{6,xx}+m_{6}*l_{6,z}^{2}$	kg*m^2
18	$I_{18}=m_{6}*(d_{2}+d_{3})*l_{6,z}$	kg*m^2
19	$I_{19}=I_{4,yy}-I_{4,xx}+I_{5,zz}-i_{5,yy}+m_{6}*l_{6,z}^{2}+I_{6,xx}-I_{6,zz}$	kg*m^2
20	$I_{20}=I_{5,yy}-I_{5,xx}-m_{6}*l_{6,z}^{2}+I_{6,zz}-I_{6,xx}$	kg*m^2
21	$I_{21}=I_{4,xx}-I_{4,yy}+I_{5,xx}-I_{5,zz}$	kg*m^2
22	$I_{22}=m_{6}*a_{3}*l_{6,z}$	kg*m^2
23	$I_{23}=I_{6,zz}$	kg*m^2

Dynamic Model 2 - Gravity

Number	Parameter	Comments
1	$g(m_{2}l_{2}+a_{2}(m_{3}+m_{4}+m_{5}+m_{6}))$	kg*m^2/s^2
2	$g(m_{3}l_{3,y}+a_{3}(m_{4}+m_{5}+m_{6}))$	kg*m^2/s^2
3	$g(m_{3}l_{3,y}+m_{4}(l_{4}+d_{4}(m_{5}+m_{6}))$	kg*m^2/s^2
4	$gl_{56}(m_{5}+m_{6})$	kg*m^2/s^2

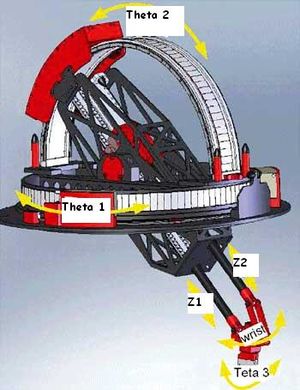
Galileo Spherical Robots (GSR)

Dynamic Model 1

Galileo robot

Number	Parameter	Comments
1	mP	Payload mass [kg]
2	mB	Balance mass [kg]
3	TP	Payload mass center distance from the flange [mm]
4	TB	Balance mass center distance from the (0,0) [mm]
5	IR	Inertia of the payload around roll [kg*m2